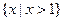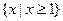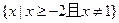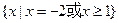题目内容
已知n为自然数,实数a>1,解关于x的不等式
logax-log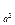 x+12log
x+12log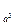 x+…+n (n-2)
x+…+n (n-2)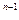 log
log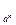 x>
x>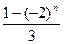 log
log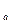 (x2-a)
(x2-a)
logax-log
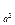 x+12log
x+12log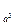 x+…+n (n-2)
x+…+n (n-2)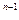 log
log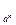 x>
x>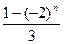 log
log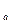 (x2-a)
(x2-a)解答见解析.
解:利用对数换底公式,原不等式左端化为
logax-4·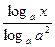 +12·
+12·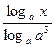 +…+n(-2)n-1 ·
+…+n(-2)n-1 ·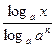
=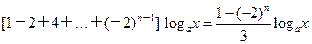
故原不等式可化为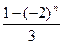 logax>
logax>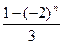 loga(x2-a). ①
loga(x2-a). ①
当n为奇数时,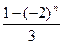 >0,不等式①等价于logax>loga(x2-a). ②
>0,不等式①等价于logax>loga(x2-a). ②
因为a>1,②式等价于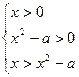
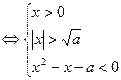
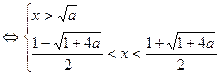 ——6分
——6分
因为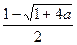 <0,
<0,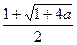 >
>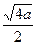 =
=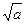 ,
,
所以,不等式②的解集为{x|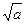 <x<
<x<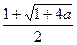 }. ——8分
}. ——8分
当n为偶数时,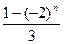 <0,不等式①等价于logax>loga(x2-a). ③
<0,不等式①等价于logax>loga(x2-a). ③
因为a>1,③式等价于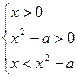
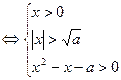
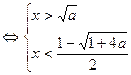 或
或 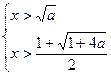 ——10分
——10分
因为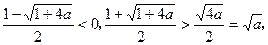 ——12分
——12分
所以,不等式③的解集为{x|x>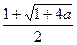 }.
}.
综合得:当n为奇数时,原不等式的解集是{x|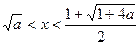 };
};
当n为偶数时,原不等式的解集是{x|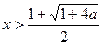 }
}
logax-4·
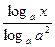 +12·
+12·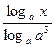 +…+n(-2)n-1 ·
+…+n(-2)n-1 ·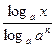
=
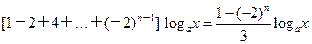
故原不等式可化为
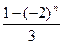 logax>
logax>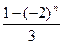 loga(x2-a). ①
loga(x2-a). ①当n为奇数时,
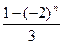 >0,不等式①等价于logax>loga(x2-a). ②
>0,不等式①等价于logax>loga(x2-a). ②因为a>1,②式等价于
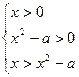
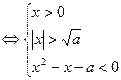
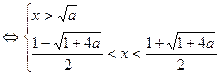 ——6分
——6分因为
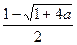 <0,
<0,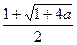 >
>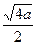 =
=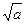 ,
,所以,不等式②的解集为{x|
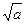 <x<
<x<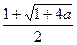 }. ——8分
}. ——8分当n为偶数时,
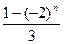 <0,不等式①等价于logax>loga(x2-a). ③
<0,不等式①等价于logax>loga(x2-a). ③因为a>1,③式等价于
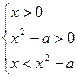
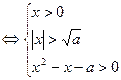
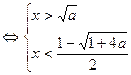 或
或 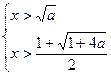 ——10分
——10分因为
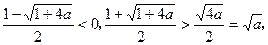 ——12分
——12分所以,不等式③的解集为{x|x>
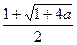 }.
}.综合得:当n为奇数时,原不等式的解集是{x|
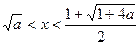 };
};当n为偶数时,原不等式的解集是{x|
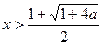 }
}
练习册系列答案
相关题目
 、
、 、
、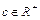 且
且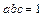 求证
求证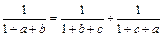 ≤1
≤1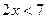 与
与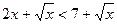
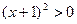 与
与
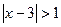 与
与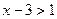
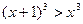 与
与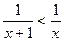
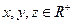 ,
,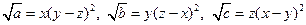 ;
;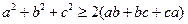 .
.
 ;
;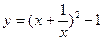 在x=____时,y有最小值____.
在x=____时,y有最小值____.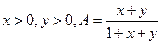 ,
, 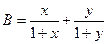 ,则
,则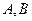 的大小关系是( )
的大小关系是( )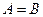
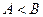
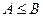
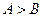
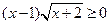 的解集是( )
的解集是( )