题目内容
已知函数f(x)=x2+bx+c,(b,c∈R),集合A={x丨f(x)=0},B={x|f(f(x)))=0},若A∩B≠∅且存在x0∈B,x0∉A则实数b的取值范围是
- A.b≠0
- B.b<0或b≥4
- C.0≤b<4
- D.b≤4或b≥4
B
分析:由f(f(x)))=0,把x2+bx+c=0代入,解得c=0,由此求得A={0,-b}.方程f(f(x)))=0即(x2+bx)(x2+bx+b)=0,解得x=0,或x=-b,或 x=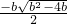 .由于存在x0∈B,x0∉A,故b2-4b≥0,从而求得实数b的取值范围.
.由于存在x0∈B,x0∉A,故b2-4b≥0,从而求得实数b的取值范围.
解答:由题意可得,A是函数f(x)的零点构成的集合.
由f(f(x)))=0,可得 (x2+bx+c)2+b(x2+bx+c)+c=0,把x2+bx+c=0代入,解得c=0.
故函数f(x)=x2+bx,故由f(x)=0可得 x=0,或x=-b,故A={0,-b}.
方程f(f(x)))=0,即 (x2+bx)2+b(x2+bx)=0,即 (x2+bx)(x2+bx+b)=0,
解得x=0,或x=-b,或 x=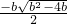 .
.
由于存在x0∈B,x0∉A,故b2-4b≥0,解得b≤0,或b≥4.
由于当b=0时,不满足集合中元素的互异性,故舍去,即实数b的取值范围为{b|b<0或b≥4 },
故选B.
点评:本题主要考查二次函数的性质,集合建的包含关系,注意检验集合中元素的互异性,属于基础题.
分析:由f(f(x)))=0,把x2+bx+c=0代入,解得c=0,由此求得A={0,-b}.方程f(f(x)))=0即(x2+bx)(x2+bx+b)=0,解得x=0,或x=-b,或 x=
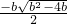 .由于存在x0∈B,x0∉A,故b2-4b≥0,从而求得实数b的取值范围.
.由于存在x0∈B,x0∉A,故b2-4b≥0,从而求得实数b的取值范围.解答:由题意可得,A是函数f(x)的零点构成的集合.
由f(f(x)))=0,可得 (x2+bx+c)2+b(x2+bx+c)+c=0,把x2+bx+c=0代入,解得c=0.
故函数f(x)=x2+bx,故由f(x)=0可得 x=0,或x=-b,故A={0,-b}.
方程f(f(x)))=0,即 (x2+bx)2+b(x2+bx)=0,即 (x2+bx)(x2+bx+b)=0,
解得x=0,或x=-b,或 x=
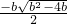 .
.由于存在x0∈B,x0∉A,故b2-4b≥0,解得b≤0,或b≥4.
由于当b=0时,不满足集合中元素的互异性,故舍去,即实数b的取值范围为{b|b<0或b≥4 },
故选B.
点评:本题主要考查二次函数的性质,集合建的包含关系,注意检验集合中元素的互异性,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|