题目内容
(本小题满分12分)
已知椭圆 的左、右两个焦点分别为F1、F2,离心率为
的左、右两个焦点分别为F1、F2,离心率为 ,且抛物线
,且抛物线 与椭圆C1有公共焦点F2(1,0)。
与椭圆C1有公共焦点F2(1,0)。
(1)求椭圆和抛物线的方程;
(2)设A、B为椭圆上的两个动点, ,过原点O作直线AB的垂线OD,垂足为D,求点D为轨迹方程。
,过原点O作直线AB的垂线OD,垂足为D,求点D为轨迹方程。
【答案】
(1)椭圆的方程为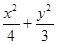 =1,抛物线的方程为
=1,抛物线的方程为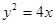
(2)点D的轨迹方程为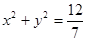
【解析】解:(1)由题意知椭圆C1中有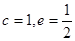
所以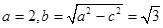
故椭圆的方程为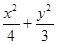 =1…………2分
=1…………2分
由F2(1,0)为抛物线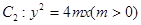 的焦点可得
的焦点可得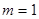
所以抛物线的方程为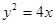 …………4分
…………4分
(2)当直线AB的斜率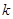 存在时
存在时
设直线AB的方程为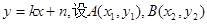
联立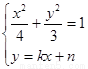
得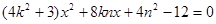 …………6分
…………6分
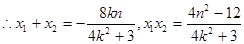
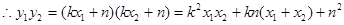
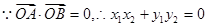
即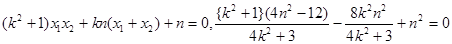
 ①…………8分
①…………8分
又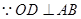 ,设
,设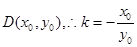 ②
②
又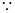 点D在直线AB上,
点D在直线AB上,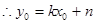
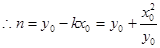 ③…………10分
③…………10分
把②③代入①得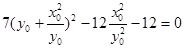
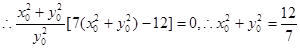
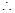 点D的轨迹方程为
点D的轨迹方程为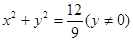
当直线AB的斜率不存在时,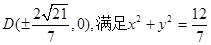
 点D的轨迹方程为
点D的轨迹方程为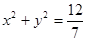 …………12分
…………12分

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目