题目内容
11.直线y=$\frac{2}{5}$x+b是曲线y=2lnx(x>0)的一条切线,则实数b=2ln5-2.分析 求出函数的导数,设出切点(m,n),求得切线的斜率,结合已知的切线方程,可得m=5,进而得到切点,代入切线方程,即可得到b.
解答 解:y=2lnx的导数为y′=$\frac{2}{x}$,
设切点为(m,n),
则曲线的切线的斜率为k=$\frac{2}{m}$,
由切线方程y=$\frac{2}{5}$x+b,
可得$\frac{2}{m}=\frac{2}{5}$,
解得m=5,
切点为(5,2ln5),
则b=2ln5-2.
故答案为:2ln5-2.
点评 本题考查导数的运用:求切线方程,主要考查导数的几何意义,设出切点和正确求导是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.运行如图所示的程序框图,输出的所有实数对(x,y)所对应的点都在函数( )
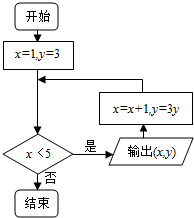

| A. | y=x+2图象上 | B. | y=3x图象上 | C. | y=3x的图象上 | D. | y=3x3图象上 |