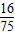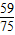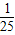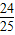题目内容
甲、乙、丙三位同学上课后独立完成5道自我检测题,甲及格概率为
,乙及格概率为
,丙及格概率为
,则三人中至少有一人及格的概率为( )
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先求出甲、乙、丙三位同学不及格的概率,三人中至少有一人及格的对立事件为三人都不及格,求出三人都不及格
则三人中至少有一人及格的概率为1减三人都不及格的概率.
则三人中至少有一人及格的概率为1减三人都不及格的概率.
解答:解:设甲及格为事件A乙及格为事件B,丙及格为事件C,则P(A)=
,P(B)=
,P(C)=
∴P(
)=
,P(
)=
,P(
)=
格,
则P(
)=P(
)P(
)P(
)=
×
×
=
∴P(ABC)=1-P(
)=
故选D
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
∴P(
. |
| A |
| 1 |
| 5 |
. |
| B |
| 3 |
| 5 |
. |
| C |
| 1 |
| 3 |
格,
则P(
. |
| ABC |
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 3 |
| 1 |
| 25 |
∴P(ABC)=1-P(
. |
| ABC |
| 24 |
| 25 |
故选D
点评:本题考查了对立事件的概率的求法,做题时认真考虑,掌握正难则反的思想.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 ,乙及格概率为
,乙及格概率为 ,丙及格概率为
,丙及格概率为 ,则三人中至少有一人及格的概率为
,则三人中至少有一人及格的概率为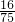
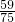


 ,乙及格概率为
,乙及格概率为 ,丙及格概率为
,丙及格概率为 ,则三人中至少有一人及格的概率为( )
,则三人中至少有一人及格的概率为( )