题目内容
为激发学生的学习兴趣,老师上课时在黑板上写出三个集合:A={x|x(mx-1)<0},B={x|2x2+x-1≤0},C={x||x|<3};然后叫甲、乙、丙三位同学到讲台上,并将“m”的值告诉了他们,要求他们各用一句话来描述,以便同学们能确定m的值.以下是甲、乙、丙三位同学的描述:甲:此数为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件.若老师评说三位同学说的都对.
(1)试求实数m的值;
(2)求(?RA)∩(B∪C).
(1)试求实数m的值;
(2)求(?RA)∩(B∪C).
分析:(1)分别求出集合A,B,C的解集,根据甲乙丙成立的条件即可求实数m的值;
(2)根据集合的基本运算即可求(?RA)∩(B∪C).
(2)根据集合的基本运算即可求(?RA)∩(B∪C).
解答:解:(1)由已知得:0<m<6且m∈N•,
∴A={x|0<x<
},
又B={x|-1≤x≤
},C={x|-3<x<3},
由乙的描述知A是B的真子集,
∴
≤
,
即m≥2,
由丙的描述知C是A的真子集,
∴m<3,
∴2≤m<3,
又m∈N•,
∴m=2.
(2)由(1)知,A={x|x(2x-1)<0}={x|0<x<
},
∴?RA={x|x≤0或x≥
},
又B∪C={x|-3<x<3},
∴(?RA)∩(B∪C)={x|-3<x≤0或
≤x<3}.
∴A={x|0<x<
| 1 |
| m |
又B={x|-1≤x≤
| 1 |
| 2 |
由乙的描述知A是B的真子集,
∴
| 1 |
| m |
| 1 |
| 2 |
即m≥2,
由丙的描述知C是A的真子集,
∴m<3,
∴2≤m<3,
又m∈N•,
∴m=2.
(2)由(1)知,A={x|x(2x-1)<0}={x|0<x<
| 1 |
| 2 |
∴?RA={x|x≤0或x≥
| 1 |
| 2 |
又B∪C={x|-3<x<3},
∴(?RA)∩(B∪C)={x|-3<x≤0或
| 1 |
| 2 |
点评:本题主要考查集合的基本运算,要求熟练掌握集合基本运算,比较基础.

练习册系列答案
相关题目
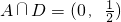 一个必要不充分条件.
一个必要不充分条件. 一个必要不充分条件.
一个必要不充分条件.