题目内容
(本小题满分14分)函数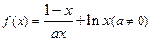 。
。
(1)求函数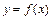 的递增区间。
的递增区间。
(2)当a=1时,求函数y=f(x)在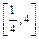 上的最大值和最小值。
上的最大值和最小值。
(3)求证: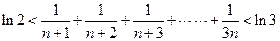
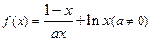 。
。(1)求函数
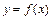 的递增区间。
的递增区间。(2)当a=1时,求函数y=f(x)在
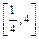 上的最大值和最小值。
上的最大值和最小值。(3)求证:
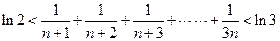
(1)

(2) f(x)max= f(
 )="3-ln4, " f(x)min= f(1)=0…
)="3-ln4, " f(x)min= f(1)=0…(3)略

(2)当a=1时,
 ……5分
……5分当x变化时,f(x),
 的变化情况如下表:
的变化情况如下表:| x |  |  | 1 |  | 4 |
 | | - | 0 | + | |
| f(x) | 3-ln4 | ↘ | 极小值 | ↗ | - +ln4 +ln4 |
 )="3-ln4, " f(1)="0 " , f(4)=-
)="3-ln4, " f(1)="0 " , f(4)=- +ln4…………7分
+ln4…………7分 f(
f( )>f(4)
)>f(4)  f(x)max= f(
f(x)max= f( )="3-ln4, " f(x)min= f(1)=0…………8分
)="3-ln4, " f(x)min= f(1)=0…………8分(3).证明:当a=1时,由(2)知f(x)≥f(1)=0

 即
即 (当且仅当x=1时取等号)………10分
(当且仅当x=1时取等号)………10分 .令
.令
即有

 当k=n+1时
当k=n+1时 
当k=n+2时

当k= 3n时

累加可得:
 …12分
…12分 .同理令
.同理令
即有

 当k=n时
当k=n时 
当k=n+1时

.
.
.
 当k= 3n时
当k= 3n时 
累加可得:

即:

故:
 ………………14分
………………14分
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 (x)= ( )
(x)= ( )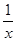 +1
+1 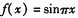 是[0,1]上的函数,且定义
是[0,1]上的函数,且定义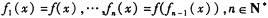 ,则满足
,则满足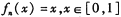 的x的个数是
的x的个数是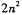
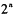
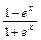 的导数为 .
的导数为 .  (
( )
)


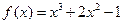 ,则
,则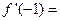 ( )。
( )。 



 的解析式可能是( )
的解析式可能是( )


