题目内容
观察等式
sin210°+sin250°+sin10°sin50°=
,
sin220°+sin240°+sin20°sin40°=
,
sin230°+sin230°+sin30°sin30°=
,
sin270°+sin2(-10°)+sin70°sin(-10°)=
(1)总结上述等式的规律,写出具有一般规律的等式;
(2)证明(1)中的具有一般规律的等式.
参考公式:sin2a=
,sin(α±β)=sinαcosβ±cosαsinβ,cos(α±β)=cosαcosβ-+sinαsinβ.
sin210°+sin250°+sin10°sin50°=
| 3 |
| 4 |
sin220°+sin240°+sin20°sin40°=
| 3 |
| 4 |
sin230°+sin230°+sin30°sin30°=
| 3 |
| 4 |
sin270°+sin2(-10°)+sin70°sin(-10°)=
| 3 |
| 4 |
(1)总结上述等式的规律,写出具有一般规律的等式;
(2)证明(1)中的具有一般规律的等式.
参考公式:sin2a=
| 1-cos2α |
| 2 |
分析:(1)各式中三角函数名称均为正弦,角的构成是满足和为60°的两角,由此写出具有一般规律的等式.
(2)应利用倍角公式、两角和与差三角函数公式证明.
(2)应利用倍角公式、两角和与差三角函数公式证明.
解答:解:(1)三角函数名称均为正弦,角的构成是满足和为60°的两角,由此具有一般规律的等式是
sin2θ+sin2(60°-θ)+sinθsin(60°-θ)=
(2)证明:左边=
+
+sinθ(sin60°cosθ-cos60°sinθ)
=1-
=1-
=
sin2θ+sin2(60°-θ)+sinθsin(60°-θ)=
| 3 |
| 4 |
(2)证明:左边=
| 1-cos2θ |
| 2 |
| 1-cos(120°-2θ) |
| 2 |
=1-
cos2θ+sin2θ×
| ||||||||||||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
点评:本题考查合情推理中的归纳猜想,属于常规要求,还利用三角函数公式进行关系式的证明,考查公式的应用能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,
, ,
,
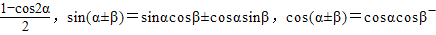 +sinαsinβ.
+sinαsinβ.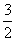 ,sin210°+sin270°+sin250°=
,sin210°+sin270°+sin250°=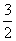 ,请写出与以上等式规律相同的一个一般化的正确等式,并给予证明。
,请写出与以上等式规律相同的一个一般化的正确等式,并给予证明。