题目内容
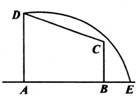 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=,曲线段DE上任一点到A、B两点的距离之和都相等.
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=,曲线段DE上任一点到A、B两点的距离之和都相等.
(1)建立适当的直角坐标系,求曲线段DE的方程;
(2)过C能否作一条直线与曲线段DE相交,且所
得弦以C为中点,如果能,求该弦所在的直线
的方程;若不能,说明理由.
证明见解析
解析:
(1)以直线AB为x轴,线段AB的中点为原点建立直角坐标系,则A(-2,0),B(2,0),C(2, ),D(-2,3).依题意,曲线段DE是以A、B为焦点的椭圆的一部分.
![]()
(2)设这样的弦存在,其方程![]() ,将其代入
,将其代入![]() ,得
,得![]()
设弦的端点为M(x1,y1),N(x2,y2),则由
![]()
∴弦MN所在直线方程为![]() 验证得知,这时
验证得知,这时![]() 适合条件.
适合条件.
故这样的直线存在,其方程为![]()

练习册系列答案
相关题目
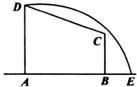 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=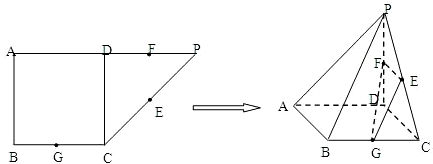
 如图所示,在直角梯形OABC中,
如图所示,在直角梯形OABC中,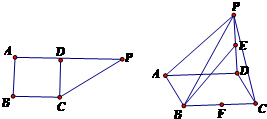 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.