题目内容
已知f(x)是定义在区间[-1,1]上的奇函数且为增函数,f(1)=1.
求(1)f(0)的值;
(2)解不等式f(x+ )<f(1-x);
)<f(1-x);
(3)若f(x)≤t2-2at+1对所有x∈[-1,1]、a∈[-1,1]恒成立,求实数t的取值范围.
解:(1)∵f(x)是定义在区间[-1,1]上的奇函数,
∴f(0)=0;…2(分)
(2)∵f(x)在区间[-1,1]上是增函数且f(x+ )<f(1-x),
)<f(1-x),
∴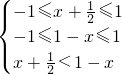 …5(分)
…5(分)
∴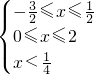 …7(分)
…7(分)
∴0≤x< ,
,
∴解集为:{x|0≤x< }…8(分)
}…8(分)
(3)f(x)max=f(1)=1…9(分)
f(x)≤t2-2at+1对所有x∈[-1,1]恒成立,则t2-2at+1≥1对a∈[-1,1]恒成立,…10(分)
构造函数f(a)=-2ta+t2,则f(a)≥0对a∈[-1,1]恒成立,
∴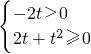 或
或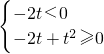 或t=0…13(分)
或t=0…13(分)
解得:t≤-2或t=0或t≥2…14(分)
分析:(1)由f(x)是定义在区间[-1,1]上的奇函数可得f(0)=0;
(2)由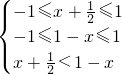 即可求得不等式f(x+
即可求得不等式f(x+ )<f(1-x)的解集;
)<f(1-x)的解集;
(3)先求得f(x)max=f(1)=1,将问题转化为:t2-2at+1≥1对a∈[-1,1]恒成立,构造函数f(a)=-2ta+t2,则f(a)≥0对a∈[-1,1]恒成立,解关于t的不等式组即可.
点评:本题考查函数恒成立问题,难点在于(3)f(x)≤t2-2at+1对所有x∈[-1,1]恒成立,转化为t2-2at+1≥f(x)max=1对a∈[-1,1]恒成立,突出考查化归思想与综合分析与应用的能力,属于难题.
∴f(0)=0;…2(分)
(2)∵f(x)在区间[-1,1]上是增函数且f(x+
 )<f(1-x),
)<f(1-x),∴
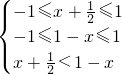 …5(分)
…5(分)∴
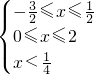 …7(分)
…7(分)∴0≤x<
 ,
,∴解集为:{x|0≤x<
 }…8(分)
}…8(分)(3)f(x)max=f(1)=1…9(分)
f(x)≤t2-2at+1对所有x∈[-1,1]恒成立,则t2-2at+1≥1对a∈[-1,1]恒成立,…10(分)
构造函数f(a)=-2ta+t2,则f(a)≥0对a∈[-1,1]恒成立,
∴
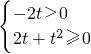 或
或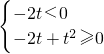 或t=0…13(分)
或t=0…13(分)解得:t≤-2或t=0或t≥2…14(分)
分析:(1)由f(x)是定义在区间[-1,1]上的奇函数可得f(0)=0;
(2)由
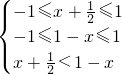 即可求得不等式f(x+
即可求得不等式f(x+ )<f(1-x)的解集;
)<f(1-x)的解集;(3)先求得f(x)max=f(1)=1,将问题转化为:t2-2at+1≥1对a∈[-1,1]恒成立,构造函数f(a)=-2ta+t2,则f(a)≥0对a∈[-1,1]恒成立,解关于t的不等式组即可.
点评:本题考查函数恒成立问题,难点在于(3)f(x)≤t2-2at+1对所有x∈[-1,1]恒成立,转化为t2-2at+1≥f(x)max=1对a∈[-1,1]恒成立,突出考查化归思想与综合分析与应用的能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目