题目内容
已知集合Sn={X|X=(x1,x2,…,xn),xi∈{0,1},i=1,2,…,n}(n≥2)对于A=(a1,a2,…an,),B=(b1,b2,…bn,)∈Sn,定义A与B的差为A-B=(|a1-b1|,|a2-b2|,…|an-bn|);A与B之间的距离为d(A,B)=
| n |
 |
| i=1 |
(Ⅰ)证明:?A,B,C∈Sn,有A-B∈Sn,且d(A-C,B-C)=d(A,B);
(Ⅱ)证明:?A,B,C∈Sn,d(A,B),d(A,C),d(B,C)三个数中至少有一个是偶数
(Ⅲ)设P⊆Sn,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
. |
| d |
证明:
. |
| d |
| mn |
| 2(m-1) |
分析:(Ⅰ)因为每个数位上都是0或者1,取差的绝对值仍然是0或者1,符合Sn的要求.
然后是减去C的数位,不管减去的是0还是1,每一个a和每一个b都是同时减去的,
因此不影响他们原先的差.
(Ⅱ)先比较A和B有几个不同(因为距离就是不同的有几个),然后比较A和C有几个不同,
这两者重复的(就是某一位上A和B不同,A和C不同,那么这一位上B和C就相同)去掉两次
(因为在前两次比较中各计算了一次),剩下的就是B和C的不同数目,
很容易得到这样的关系式:h=k+l-2i,从而三者不可能同为奇数.
(Ⅲ)首先理解P中会出现Cm2个距离,所以平均距离就是距离总和再除以Cm2,
而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,
第二位一共产生了多少个不同,如此下去,直到第n位.然后思考,
第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,
等算出来t1(m-t1)≤
,一切就水到渠成了.
此外,这个问题需要注意一下数学语言的书写规范.
然后是减去C的数位,不管减去的是0还是1,每一个a和每一个b都是同时减去的,
因此不影响他们原先的差.
(Ⅱ)先比较A和B有几个不同(因为距离就是不同的有几个),然后比较A和C有几个不同,
这两者重复的(就是某一位上A和B不同,A和C不同,那么这一位上B和C就相同)去掉两次
(因为在前两次比较中各计算了一次),剩下的就是B和C的不同数目,
很容易得到这样的关系式:h=k+l-2i,从而三者不可能同为奇数.
(Ⅲ)首先理解P中会出现Cm2个距离,所以平均距离就是距离总和再除以Cm2,
而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,
第二位一共产生了多少个不同,如此下去,直到第n位.然后思考,
第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,
等算出来t1(m-t1)≤
| m2 |
| 4 |
此外,这个问题需要注意一下数学语言的书写规范.
解答:解:(1)设A=(a1,a2,…,an),B=(b1,b2,…,bn),C=(c1,c2,…,cn)∈Sn
因ai,bi∈0,1,故|ai-bi|∈0,1,(i=1,2,…,n)a1b1∈0,1,
即A-B=(|a1-b1|,|a2-b2|,…,|an-bn|)∈Sn
又ai,bi,ci∈(0,1),i=1,2,…,n
当ci=0时,有||ai-ci|-|bi-ci||=|ai-bi|;
当ci=1时,有||ai-ci|-|bi-ci||=|(1-ai)-(1-bi)=|ai-bi|
故d(A-C,B-C)=
|ai-bi|=d(A,B)
(2)设A=(a1,a2,…,an),B=(b1,b2,…,bn),C=(c1,c2,…,cn)∈Sn
记d(A,B)=k,d(A,C)=l,d(B,C)=h
记O=(0,0,…,0)∈Sn,由第一问可知:
d(A,B)=d(A-A,B-A),d=(O,B-A)=k
d(A,C)=d(A-A,C-A)=d(O,C-A)=l
d(B,C)=d(B-A,C-A)=h
即|bi-ai|中1的个数为k,|ci-ai|中1的个数为l,(i=1,2,…,n)
设t是使|bi-ai|=|ci-ai|=1成立的i的个数,则有h=k+l-2t,
由此可知,k,l,h不可能全为奇数,即d(A,B),d(A,C),d(B,C)三个数中至少有一个是偶数.
(3)显然P中会产生Cm2个距离,也就是说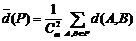 ,其中
,其中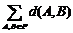 表示P中每两个元素距离的总和.
表示P中每两个元素距离的总和.
分别考察第i个位置,不妨设P中第i个位置一共出现了ti个1,那么自然有m-ti个0,因此在这个位置上所产生的距离总和为ti(m-ti)≤
,(i=1,2,…,n),
那么n个位置的总和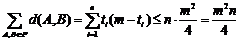
即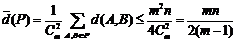
因ai,bi∈0,1,故|ai-bi|∈0,1,(i=1,2,…,n)a1b1∈0,1,
即A-B=(|a1-b1|,|a2-b2|,…,|an-bn|)∈Sn
又ai,bi,ci∈(0,1),i=1,2,…,n
当ci=0时,有||ai-ci|-|bi-ci||=|ai-bi|;
当ci=1时,有||ai-ci|-|bi-ci||=|(1-ai)-(1-bi)=|ai-bi|
故d(A-C,B-C)=
| n | ||
|
(2)设A=(a1,a2,…,an),B=(b1,b2,…,bn),C=(c1,c2,…,cn)∈Sn
记d(A,B)=k,d(A,C)=l,d(B,C)=h
记O=(0,0,…,0)∈Sn,由第一问可知:
d(A,B)=d(A-A,B-A),d=(O,B-A)=k
d(A,C)=d(A-A,C-A)=d(O,C-A)=l
d(B,C)=d(B-A,C-A)=h
即|bi-ai|中1的个数为k,|ci-ai|中1的个数为l,(i=1,2,…,n)
设t是使|bi-ai|=|ci-ai|=1成立的i的个数,则有h=k+l-2t,
由此可知,k,l,h不可能全为奇数,即d(A,B),d(A,C),d(B,C)三个数中至少有一个是偶数.
(3)显然P中会产生Cm2个距离,也就是说
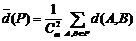 ,其中
,其中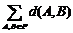 表示P中每两个元素距离的总和.
表示P中每两个元素距离的总和.分别考察第i个位置,不妨设P中第i个位置一共出现了ti个1,那么自然有m-ti个0,因此在这个位置上所产生的距离总和为ti(m-ti)≤
| m2 |
| 4 |
那么n个位置的总和
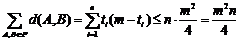
即
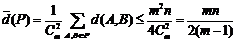
点评:本题是综合考查集合、数列与推理综合的应用,这道题目的难点主要出现在读题上,需要仔细分析,以找出解题的突破点.题目所给的条件其实包含两个定义,第一个是关于Sn的,其实Sn中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1,第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了.

练习册系列答案
相关题目