题目内容
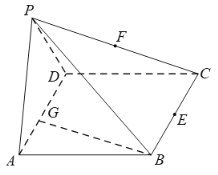
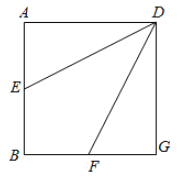
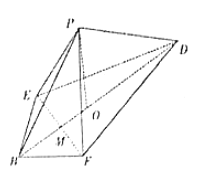
【题目】如图,已知四棱锥![]() 的底面为边长为
的底面为边长为![]() 的菱形,
的菱形,![]() 为
为![]() 中点,连接
中点,连接![]() .
.
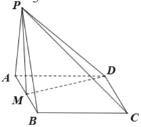
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,且二面角
,且二面角![]() 的余弦值为
的余弦值为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见证明;(Ⅱ)2.
【解析】
(Ⅰ)连接![]() ,在菱形
,在菱形![]() 中可得
中可得![]() ,又
,又![]() ,进而可得
,进而可得![]() 平面
平面![]() ,于是得到
,于是得到![]() 平面
平面![]() ,所以可得结论成立.(Ⅱ)建立空间直角坐标系,设
,所以可得结论成立.(Ⅱ)建立空间直角坐标系,设![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() 可得
可得![]() ,即
,即![]() ,然后根据椎体的体积公式求解即可.
,然后根据椎体的体积公式求解即可.
(Ⅰ)连接![]() ,
,
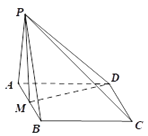
∵菱形![]() 中,
中,![]() ,
,
∴![]() 为等边三角形,又
为等边三角形,又![]() 为
为![]() 中点,
中点,
∴![]() .
.
又![]() ,则
,则![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)∵平面![]()
![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,
则![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则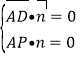 ,即
,即![]() ,可取
,可取![]()
又平面![]() 的法向量可取
的法向量可取![]() ,
,
由题意得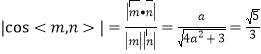 ,
,
解得![]() ,即
,即![]() ,
,
又菱形![]() 的面积
的面积![]() ,
,
∴四棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目
【题目】画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了合理定价,先进行试销售,其单价x(元)与销量y(个)相关数据如表:
单价x(元) | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量y(个) | 12 | 11 | 9 | 7 | 6 |
(1)已知销量y与单价x具有线性相关关系,求y关于x的线性回归方程;
(2)若该新造型糖画每个的成本为5.7元,要使得进入售卖时利润最大,请利用所求出的线性回归方程确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程y![]() x中斜率和截距最小二乘法估计计算公式:
x中斜率和截距最小二乘法估计计算公式: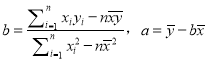 .参考数据:
.参考数据:![]() .
.