题目内容
某厂家举行大型的促销活动,经测算某产品当促销费用为x万元时,销售量P万件满足P=3-
(其中0≤x≤a,a为正常数).现假定生产量与销售量相等,已知生产该产品P万件还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为(4+
)万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
| 2 |
| x+1 |
| 20 |
| P |
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
分析:(1)根据题意售价为(4+
)万元/万件,销售量为P,成本为(10+2P)+x万元,利用利润=销售额-成本,即可列出函数关系式;
(2)对a进行分类讨论,当a≥1时,利用基本不等式即可求得最值,当a<1时,利用导数确定函数的单调性,从而求得最值,即可得到答案.
| 20 |
| P |
(2)对a进行分类讨论,当a≥1时,利用基本不等式即可求得最值,当a<1时,利用导数确定函数的单调性,从而求得最值,即可得到答案.
解答:解:(1)由题意知,该产品售价为2×(
)万元,销售量为P,成本为(10+2P)+x万元,
∴y=2×(
)×P-10-2P-x,
∵P=3-
(其中0≤x≤a,a为正常数),
∴y=2×
×(3-
)-10-2×(3-
)-x=16-x-
,
∴y=16-(
+x)(0≤x≤a),
∴该产品的利润y万元表示为促销费用x万元的函数为y=16-(
+x)(0≤x≤a);
(2)由(1)可知,y=16-(
+x)(0≤x≤a),
∴y=17-(
+x+1)≤17-2
=13,
当且仅当
=x+1,即x=1时取等号,
∵0≤x≤a,
①当a≥1时,x=1时,y取得最大值为13,
∴促销费用投入1万元时,厂家的利润最大;
②当a<1时,y=16-(
+x),
∴y′=
>0,解得-3<x<1,
∴y=17-(
+x+1)在(-3,1)上单调递增,
∴y=17-(
+x+1)在[0,a]上单调递增,
∴在x=a时,函数有最大值,
∴促销费用投入a万元时,厂家的利润最大.
综合①②可得,当a≥1时,促销费用投入1万元时,厂家的利润最大,
当a<1时,促销费用投入a万元时,厂家的利润最大.
| 10+2P |
| P |
∴y=2×(
| 10+2P |
| P |
∵P=3-
| 2 |
| x+1 |
∴y=2×
10+2(3-
| ||
3-
|
| 2 |
| x+1 |
| 2 |
| x+1 |
| 4 |
| x+1 |
∴y=16-(
| 4 |
| x+1 |
∴该产品的利润y万元表示为促销费用x万元的函数为y=16-(
| 4 |
| x+1 |
(2)由(1)可知,y=16-(
| 4 |
| x+1 |
∴y=17-(
| 4 |
| x+1 |
|
当且仅当
| 4 |
| x+1 |
∵0≤x≤a,
①当a≥1时,x=1时,y取得最大值为13,
∴促销费用投入1万元时,厂家的利润最大;
②当a<1时,y=16-(
| 4 |
| x+1 |
∴y′=
| -(x-1)•(x+3) |
| (x+1)2 |
∴y=17-(
| 4 |
| x+1 |
∴y=17-(
| 4 |
| x+1 |
∴在x=a时,函数有最大值,
∴促销费用投入a万元时,厂家的利润最大.
综合①②可得,当a≥1时,促销费用投入1万元时,厂家的利润最大,
当a<1时,促销费用投入a万元时,厂家的利润最大.
点评:本题主要考查函数模型的选择与应用.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.在运用数学方法求解最值时,选用了基本不等式和导数的方法求解.属于中档题.

练习册系列答案
相关题目
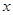 万元满足
万元满足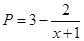 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为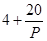 元.
元.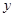 万元表示为促销费用
万元表示为促销费用