题目内容
4.双曲线$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{m}$=1的离心率e=2,则双曲线的渐近线方程为y=±$\frac{\sqrt{3}}{3}$x.分析 由离心率公式解出m,再由双曲线方程写出渐近线方程即可.
解答 解:双曲线$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{m}$=1的离心率e=2,
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,
∴22=1+$\frac{m}{16}$,
解得m=48,
∴$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{48}$=1,
∴双曲线的渐近线方程为y=±$\frac{\sqrt{3}}{3}$x,
故答案为:y=±$\frac{\sqrt{3}}{3}$x.
点评 本题考查双曲线的方程和性质,主要是渐近线方程,考查运算能力,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
14.不论m如何变化,直线(m+2)x-(2m-1)y-(3m-4)=0恒过定点( )
| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
12.设集合M={x|x≤2$\sqrt{3}$},a=$\sqrt{11+b}$,b∈(0,1),则下列关系中正确的是( )
| A. | a⊆M | B. | a∉M | C. | {a}∈M | D. | {a}⊆M |
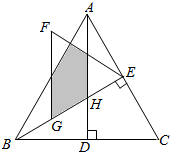 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{{5\sqrt{3}}}{2}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{{5\sqrt{3}}}{2}$.