题目内容
已知函数![]() 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为![]() ,函数
,函数![]() .
.
(1)若函数g(x)在x=1处有极值,求g(x)的解析式;
(2)若函数g(x)在区间[﹣1,1]上为增函数,且b2﹣mb+4≥g(x)在x∈[﹣1,1]时恒成立,求实数m的取值范围.
考点:
利用导数研究函数的极值;函数解析式的求解及常用方法;函数恒成立问题;直线的斜率.
专题:
计算题.
分析:
(1)先求出斜率为3的切线方程,根据两条切线间的距离求出a值,再讨论满足g′(x)=0的点附近的导数的符号的变化情况,来确定极值,求出b即可.
(2)欲使函数g(x)在区间[﹣1,1]上为增函数只需转化成g′(x)≥0在区间[﹣1,1]上恒成立,求出b的范围,根据g(x)在x∈[﹣1,1]是增函数知g(x)的最大值为g(1),只需使b2﹣mb+4≥g(1)恒成立即可.
解答:
解:(1)∵![]() ,
,
∴由![]() =3得x=±a,
=3得x=±a,
即切点坐标为(a,a),(﹣a,﹣a)
∴切线方程为y﹣a=3(x﹣a),或y+a=3(x+a)(2分)
整理得3x﹣y﹣2a=0或3x﹣y+2a=0
∴![]() ,
,
解得a=±1,
∴f(x)=x3.
∴g(x)=x3﹣3bx+3(4分)
∵g′(x)=3x2﹣3b,g(x)在x=1处有极值,
∴g′(1)=0,
即3×12﹣3b=0,解得b=1
∴g(x)=x3﹣3x+3(6分)
(2)∵函数g(x)在区间[﹣1,1]上为增函数,
∴g′(x)=3x2﹣3b≥0在区间[﹣1,1]上恒成立,
∴b≤0,
又∵b2﹣mb+4≥g(x)在区间[﹣1,1]上恒成立,
∴b2﹣mb+4≥g(1)(8分)
即b2﹣mb+4≥4﹣3b,若b=0,则不等式显然成立,若b≠0,
则m≥b+3在b∈(﹣∞,0)上恒成立
∴m≥3.
故m的取值范围是[3,+∞)
点评:
本题主要考查了利用导数研究函数极值,以及函数恒成立问题和利用待定系数法求解析式,属于基础题.

 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为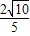 ,函数
,函数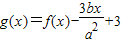 .
.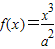 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为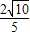 ,函数
,函数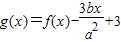 .
. 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为 ,函数
,函数 。
。 在
在 处有极值,求
处有极值,求 在
在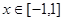 时恒成立,求实数
时恒成立,求实数 的取值范围。
的取值范围。