题目内容
(本小题满分12分)
已知椭圆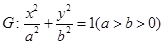 的离心率为
的离心率为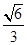 ,右焦点为
,右焦点为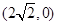 。斜率为1的直线
。斜率为1的直线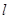 与椭圆
与椭圆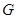 交于
交于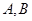 两点,以
两点,以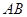 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为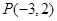 。
。
(Ⅰ)求椭圆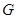 的方程;
的方程;
(Ⅱ)求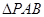 的面积。
的面积。
【答案】
(1) 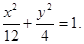 (2) S=
(2) S=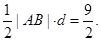
【解析】
试题分析:(Ⅰ)由已知得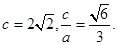 解得
解得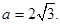 又
又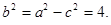
所以椭圆G的方程为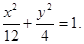
(Ⅱ)设直线l的方程为 由
由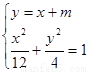 得
得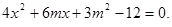 设A、B的坐标分别为
设A、B的坐标分别为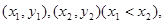 AB中点为E
AB中点为E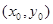 ,则
,则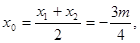
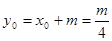 因为AB是等腰△PAB的底边,所以PE⊥AB.所以PE的斜率
因为AB是等腰△PAB的底边,所以PE⊥AB.所以PE的斜率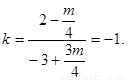 解得m=2。此时方程①为
解得m=2。此时方程①为 解得
解得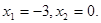 所以
所以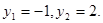 所以|AB|=
所以|AB|=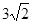 .此时,点P(—3,2)到直线AB:
.此时,点P(—3,2)到直线AB: 的距离
的距离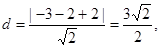 所以△PAB的面积S=
所以△PAB的面积S=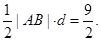
考点:直线与椭圆的位置关系
点评:解决该试题的关键是能利用性质得到方程,同时能利用联立方程组和韦达定理来得到直线的斜率,以及点到直线的距离公式得到面积的表示,属于基础题。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目