题目内容
设函数f(x)=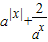 (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2
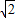 );
);(2)若函数f(x)在(-∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
【答案】分析:(1)当a=10时,f(x)=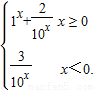 按照分段函数选择解析式,
按照分段函数选择解析式,
①当x<0时,f(x)=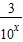 >3.因为m>2
>3.因为m>2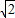 .所以当2
.所以当2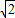 <m≤3时,方程f(x)=m无解;当m>3,由10x=
<m≤3时,方程f(x)=m无解;当m>3,由10x=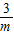 求解.
求解.
②当x≥0时,10x≥1.由f(x)=m得10x+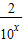 =m,转化为(10x)2-m10x+2=0.求解.
=m,转化为(10x)2-m10x+2=0.求解.
(2)根据题意有g(x)=a|x|+2ax,x∈[-2,+∞),根据指数函数,分①当a>1时,②当0<a<1时,两种情况分析,每种情况下,根据绝对值,再按照x≥0时和-2≤x<0两种情况讨论.最后综合取并集.
解答:解:(1)f(x)=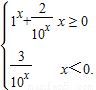 (2分)
(2分)
①当x<0时,f(x)=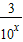 >3.因为m>2
>3.因为m>2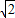 .
.
则当2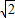 <m≤3时,方程f(x)=m无解;
<m≤3时,方程f(x)=m无解;
当m>3,由10x=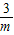 ,得x=lg
,得x=lg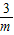 .(4分)
.(4分)
②当x≥0时,10x≥1.由f(x)=m得10x+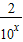 =m,
=m,
∴(10x)2-m10x+2=0.
因为m>2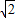 ,判别式△=m2-8>0,解得10x=
,判别式△=m2-8>0,解得10x=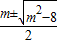 .
.
因为m>2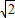 ,所以
,所以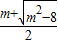 >
>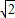 >1.
>1.
所以由10x= ,解得x=lg
,解得x=lg .
.
令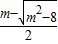 =1,得m=3.
=1,得m=3.
所以当m>3时,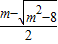 =
=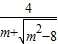 <
<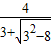 =1,
=1,
当2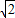 <m≤3时,
<m≤3时,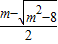 =
=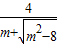 >
>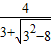 =1,解得x=lg
=1,解得x=lg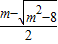 .
.
综上,当m>3时,方程f(x)=m有两解x=lg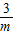 和x=lg
和x=lg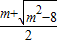 ;
;
当2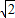 <m≤3时,方程f(x)=m有两解x=lg
<m≤3时,方程f(x)=m有两解x=lg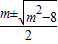 .(8分)
.(8分)
(2)①若0<a<1,
当x<0时,0<f(x)=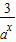 <3;
<3;
当0≤x≤2时,f(x)=ax+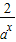 .
.
令t=ax,则t∈[a2,1],g(t)=t+ 在[a2,1]上单调递减,
在[a2,1]上单调递减,
所以当t=1,即x=0时f(x)取得最小值为3.
当t=a2时,f(x)取得最大值为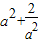 .
.
此时f(x)在(-∞,2]上的值域是(0,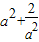 ],没有最小值.(11分)
],没有最小值.(11分)
②若a>1,
当x<0时,f(x)=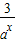 >3;
>3;
当0≤x≤2时f(x)=ax+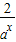 .
.
令t=ax,g(t)=t+ ,则t∈[1,a2].
,则t∈[1,a2].
①若a2≤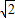 ,g(t)=t+
,g(t)=t+ 在[1,a2]上单调递减,
在[1,a2]上单调递减,
所以当t=a2即x=2时f(x)取最小值a2+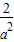 ,最小值与a有关;(13分)
,最小值与a有关;(13分)
②a2>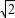 ,g(t)=t+
,g(t)=t+ 在[1,
在[1,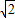 ]上单调递减,在[
]上单调递减,在[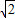 ,a2]上单调递增,
,a2]上单调递增,
所以当t=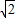 即x=loga
即x=loga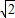 时f(x)取最小值2
时f(x)取最小值2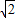 ,最小值与a无关.(15分)
,最小值与a无关.(15分)
综上所述,当a≥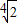 时,f(x)在(-∞,2]上的最小值与a无关.(16分)
时,f(x)在(-∞,2]上的最小值与a无关.(16分)
点评:本题主要考查了函数与方程的综合运用,主要涉及了方程的根,函数的最值等问题,还考查了分类讨论思想,转化思想.
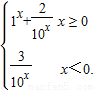 按照分段函数选择解析式,
按照分段函数选择解析式,①当x<0时,f(x)=
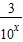 >3.因为m>2
>3.因为m>2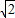 .所以当2
.所以当2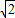 <m≤3时,方程f(x)=m无解;当m>3,由10x=
<m≤3时,方程f(x)=m无解;当m>3,由10x=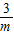 求解.
求解.②当x≥0时,10x≥1.由f(x)=m得10x+
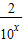 =m,转化为(10x)2-m10x+2=0.求解.
=m,转化为(10x)2-m10x+2=0.求解.(2)根据题意有g(x)=a|x|+2ax,x∈[-2,+∞),根据指数函数,分①当a>1时,②当0<a<1时,两种情况分析,每种情况下,根据绝对值,再按照x≥0时和-2≤x<0两种情况讨论.最后综合取并集.
解答:解:(1)f(x)=
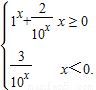 (2分)
(2分)①当x<0时,f(x)=
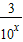 >3.因为m>2
>3.因为m>2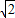 .
.则当2
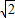 <m≤3时,方程f(x)=m无解;
<m≤3时,方程f(x)=m无解;当m>3,由10x=
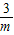 ,得x=lg
,得x=lg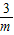 .(4分)
.(4分)②当x≥0时,10x≥1.由f(x)=m得10x+
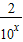 =m,
=m,∴(10x)2-m10x+2=0.
因为m>2
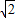 ,判别式△=m2-8>0,解得10x=
,判别式△=m2-8>0,解得10x=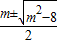 .
.因为m>2
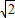 ,所以
,所以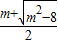 >
>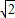 >1.
>1.所以由10x=
 ,解得x=lg
,解得x=lg .
.令
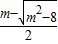 =1,得m=3.
=1,得m=3.所以当m>3时,
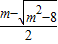 =
=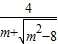 <
<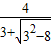 =1,
=1,当2
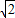 <m≤3时,
<m≤3时,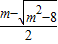 =
=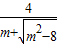 >
>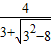 =1,解得x=lg
=1,解得x=lg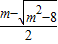 .
.综上,当m>3时,方程f(x)=m有两解x=lg
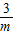 和x=lg
和x=lg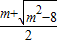 ;
;当2
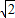 <m≤3时,方程f(x)=m有两解x=lg
<m≤3时,方程f(x)=m有两解x=lg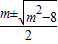 .(8分)
.(8分)(2)①若0<a<1,
当x<0时,0<f(x)=
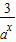 <3;
<3;当0≤x≤2时,f(x)=ax+
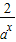 .
.令t=ax,则t∈[a2,1],g(t)=t+
 在[a2,1]上单调递减,
在[a2,1]上单调递减,所以当t=1,即x=0时f(x)取得最小值为3.
当t=a2时,f(x)取得最大值为
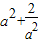 .
.此时f(x)在(-∞,2]上的值域是(0,
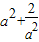 ],没有最小值.(11分)
],没有最小值.(11分)②若a>1,
当x<0时,f(x)=
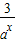 >3;
>3;当0≤x≤2时f(x)=ax+
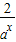 .
.令t=ax,g(t)=t+
 ,则t∈[1,a2].
,则t∈[1,a2].①若a2≤
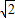 ,g(t)=t+
,g(t)=t+ 在[1,a2]上单调递减,
在[1,a2]上单调递减,所以当t=a2即x=2时f(x)取最小值a2+
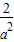 ,最小值与a有关;(13分)
,最小值与a有关;(13分)②a2>
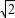 ,g(t)=t+
,g(t)=t+ 在[1,
在[1,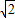 ]上单调递减,在[
]上单调递减,在[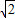 ,a2]上单调递增,
,a2]上单调递增,所以当t=
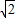 即x=loga
即x=loga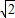 时f(x)取最小值2
时f(x)取最小值2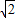 ,最小值与a无关.(15分)
,最小值与a无关.(15分)综上所述,当a≥
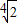 时,f(x)在(-∞,2]上的最小值与a无关.(16分)
时,f(x)在(-∞,2]上的最小值与a无关.(16分)点评:本题主要考查了函数与方程的综合运用,主要涉及了方程的根,函数的最值等问题,还考查了分类讨论思想,转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目