题目内容
已知实数a1,a2,a3不全为零,(i)则
| a1a2+2a2a3 | ||||||
|
(ii)设正数x,y满足x+y=2,令
| xa1a2+ya2a3 | ||||||
|
分析:观察分式的分子和分母的代数式的不同,进行拆分a22项,构造均值不等式求最值.
解答:解:由题意知:
(1)
=
≤
=
=
(2)
=
≤
=
∴M=
即M≥
(
)=
∴M的最小值为
.
故(1)
(2)
(1)
| a1a2+2a2a3 | ||||||
|
| a1a2+2a2a3 | ||||||||||||
|
≤
| a1a2+2a2a3 | ||||||||||||||||
2
|
| a1a2+2a2a3 | ||||
|
=
| ||
| 2 |
(2)
| xa1a2+ya2a3 | ||||||
|
| xa1a2+ya2a3 | ||||||||||||
|
≤
| xa1a2+ya2a3 | ||||||||
2
|
| ||
| 2 |
∴M=
| ||
| 2 |
即M≥
| ||
| 2 |
| x+y |
| 2 |
| ||
| 2 |
∴M的最小值为
| ||
| 2 |
故(1)
| ||
| 2 |
| ||
| 2 |
点评:本题对均值不等式的灵活熟练运用的程度要求比较高,属中档偏上题型.

练习册系列答案
相关题目
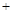 a2
a2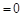 ,a1a42
,a1a42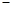 a2
a2 a2
a2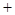 a2
a2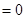 ,a1a42
,a1a42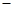 a2
a2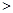 a2
a2