题目内容
函数y=2-x（-1≤x≤3）的值域是（ ）
分析：由于函数y=2-x =(
)x 在R上是减函数，且-1≤x≤3，利用单调性求得函数的值域．
| 1 |
| 2 |
解答：解：由于函数y=2-x =(
)x 在R上是减函数，且-1≤x≤3，故当x=3时，函数取得最小值为
，
当x=-1时，函数取得最大值为 2，故函数的值域为 [
，2]，
故选B．
| 1 |
| 2 |
| 1 |
| 8 |
当x=-1时，函数取得最大值为 2，故函数的值域为 [
| 1 |
| 8 |
故选B．
点评：本题主要考查指数函数的单调性，求函数的值域，属于中档题．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
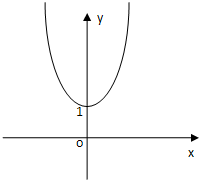已知函数y=2|x|