题目内容
 已知函数y=2|x|
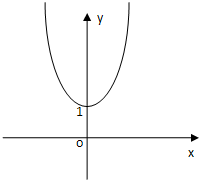
已知函数y=2|x|(1)作出其图象;
(2)由图象指出单调区间;
(3)由图象指出当x取何值时函数有最小值,最小值为多少?
分析:(1)根据函数y=2|x|的是偶函数,在(0,+∞)上是增函数,且它的图象经过点(0,1),图象关于y轴对称,画出它的图象.
(2)结合函数的图象,可得函数的减区间和增区间.
(3)数形结合可得,当x=0时,ymiin=20,计算求得结果.
(2)结合函数的图象,可得函数的减区间和增区间.
(3)数形结合可得,当x=0时,ymiin=20,计算求得结果.
解答: 解:(1)函数y=2|x|的是偶函数,在(0,+∞)上是增函数,且它的图象经过点(0,1),
解:(1)函数y=2|x|的是偶函数,在(0,+∞)上是增函数,且它的图象经过点(0,1),
它的图象关于y轴对称,如图所示:
(2)结合函数的图象,可得函数的减区间为(-∞,0],增区间为(0,+∞).
(3)数形结合可得,当x=0时,ymiin=20=1.
 解:(1)函数y=2|x|的是偶函数,在(0,+∞)上是增函数,且它的图象经过点(0,1),
解:(1)函数y=2|x|的是偶函数,在(0,+∞)上是增函数,且它的图象经过点(0,1),它的图象关于y轴对称,如图所示:
(2)结合函数的图象,可得函数的减区间为(-∞,0],增区间为(0,+∞).
(3)数形结合可得,当x=0时,ymiin=20=1.
点评:本题主要考查指数函数的图象和性质综合,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
已知函数y=
的定义域为M,集合N={y|y>1},则M∩N=( )
| 2-x |
| A、[0,2) |
| B、(0,2) |
| C、(1,2] |
| D、[1,2) |