题目内容
设曲线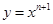 (
(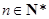 )在点(1,1)处的切线与x轴的交点的横坐标为
)在点(1,1)处的切线与x轴的交点的横坐标为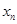 ,则
,则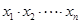 = .
= .
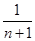
解析试题分析:f′(x)=(n+1)xn,
k=f′(x)=n+1,
点P(1,1)处的切线方程为:y-1=(n+1)(x-1),
令y=0得,x=1-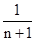 =
=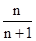 ,
,
即xn=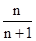 ,
,
∴x1×x2×…×x2011×xn=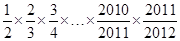 ×
×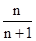 =
=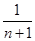
考点:本题主要考查导数的几何意义;数列“累乘法”.
点评:利用导数求曲线上某点的切线方程,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
函数 的实数解落在的区间是( )
的实数解落在的区间是( )
A.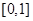 | B.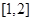 | C. | D.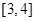 |
 ,则
,则 =_______.
=_______. (
(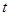 的单位为:秒,
的单位为:秒,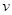 的单位为:米/秒)的速度作变速直线运动,则该物体从时刻
的单位为:米/秒)的速度作变速直线运动,则该物体从时刻 秒至时刻
秒至时刻 秒间运动的路程
秒间运动的路程  中,
中, ,
, ,若数列
,若数列 满足
满足 ,则数列
,则数列 的前
的前 项和
项和 .
.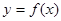 在点P处的切线方程是
在点P处的切线方程是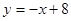 ,则
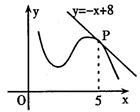
,则 =
= 
 ,若
,若 ,则
,则 .
. 与
与 轴及直线
轴及直线 围成的图形面积为
围成的图形面积为 ,则m的值为 .
,则m的值为 . 在区间
在区间 上恰有一个极值点,则实数
上恰有一个极值点,则实数 的取值范围是
的取值范围是