Question

函数y＝cos(－2x)的单调递增区间是    （   ）

A．[k＋，kπ＋]	B．[k－，k＋]
C．[2k＋，2k＋]	D．[2k－，2kπ＋]（以上k∈Z）

Answer 1

B

解析试题分析：y＝cos(－2x)即y＝cos(2x－)。由
得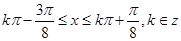，，所以，函数y＝cos(－2x)的单调递增区间
是[k－，k＋]，故选B。
考点：本题主要考查余弦函数的单调性，复合函数的单调性。
点评：易错题，复合函数的单调性判断，依据“内外层函数，同增异减”。