题目内容
(12分)假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间
(1)你离家前不能看到报纸(称事件A)的概率是多少?(6分,须有过程)
(2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)(6分)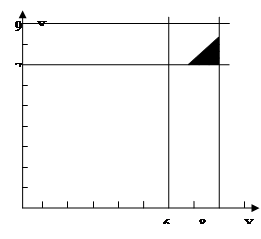
(1)你离家前不能看到报纸(称事件A)的概率是多少?(6分,须有过程)
(2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)(6分)

答:(1)小王离家前不能看到报纸的概率是0.125。
(2)用计算机产生随机数摸拟试验,X是0—1之间的均匀随机数,Y也是0—1之间的均匀随机数,各产生100个。依序计算,如果满足2X+6>2y+7,那小王离家前不能看到报纸,统计共有多少为M,则M/100即为估计的概率。本题属于几何概型的概率问题。要先计算出试验对应区域的面积,然后计算出事件对应的区域的面积。最后作商即可。
如图,设送报人到达的时间为X,你离家去工作的时间为Y。(X,Y)可以看成平面中的点,试验的全部结果所构成的区域为 一个正方形区域,面积为SΩ=4,事件A表示小王离家前不能看到报纸,所构成的区域为A={(X,Y)/
一个正方形区域,面积为SΩ=4,事件A表示小王离家前不能看到报纸,所构成的区域为A={(X,Y)/  即图中的阴影部分,面积为SA=0.5。这是一个几何概型,所以P(A)=SA/SΩ=0.5/4=0.125。
即图中的阴影部分,面积为SA=0.5。这是一个几何概型,所以P(A)=SA/SΩ=0.5/4=0.125。
答:小王离家前不能看到报纸的概率是0.125。(6分)
(2)用计算机产生随机数摸拟试验,X是0—1之间的均匀随机数,Y也是0—1之间的均匀随机数,各产生100个。依序计算,如果满足2X+6>2y+7,那小王离家前不能看到报纸,统计共有多少为M,则M/100即为估计的概率。(12分)
如图,设送报人到达的时间为X,你离家去工作的时间为Y。(X,Y)可以看成平面中的点,试验的全部结果所构成的区域为
 一个正方形区域,面积为SΩ=4,事件A表示小王离家前不能看到报纸,所构成的区域为A={(X,Y)/
一个正方形区域,面积为SΩ=4,事件A表示小王离家前不能看到报纸,所构成的区域为A={(X,Y)/  即图中的阴影部分,面积为SA=0.5。这是一个几何概型,所以P(A)=SA/SΩ=0.5/4=0.125。
即图中的阴影部分,面积为SA=0.5。这是一个几何概型,所以P(A)=SA/SΩ=0.5/4=0.125。答:小王离家前不能看到报纸的概率是0.125。(6分)
(2)用计算机产生随机数摸拟试验,X是0—1之间的均匀随机数,Y也是0—1之间的均匀随机数,各产生100个。依序计算,如果满足2X+6>2y+7,那小王离家前不能看到报纸,统计共有多少为M,则M/100即为估计的概率。(12分)

练习册系列答案
相关题目
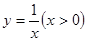 图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为 ( )
图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为 ( )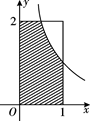
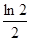
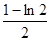
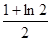
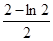
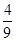 附近,那么点A和点C到直线BD的距离之比约为 .
附近,那么点A和点C到直线BD的距离之比约为 .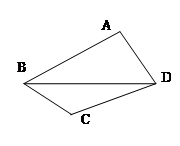
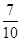
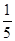
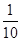
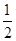
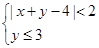 所表示的平面区域内的概率为( )
所表示的平面区域内的概率为( )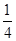
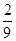
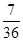
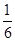
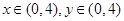 .
.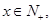
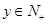 以
以 作为矩形的边长,记矩形的面积为
作为矩形的边长,记矩形的面积为 ,求
,求 的概率;
的概率; 求这两数之差不大于2的概率.
求这两数之差不大于2的概率. 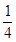

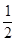
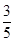
 的圆依次相切,右边正方形内有一个半径为a的内切圆,在这两个图形上各随机撒一粒黄豆,落在阴影内的概率分别为
的圆依次相切,右边正方形内有一个半径为a的内切圆,在这两个图形上各随机撒一粒黄豆,落在阴影内的概率分别为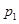 ,
, ,则
,则