题目内容
函数y=sin22x是( )
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
分析:先将函数运用二倍角公式化简为y=Asin(wx+ρ)的形式,再利用正弦函数的性质可得答案.
解答:解:∵f(x)=sin22x=
-
cos4x∴f(-x)=
-
cos(-4x )=
-
cos4x=f(x)为偶函数
T=
=
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
T=
| 2π |
| 4 |
| π |
| 2 |
故选D.
点评:本题主要考查三角函数的奇偶性和最小正周期的求法.一般都要把三角函数化简为y=Asin(wx+ρ)的形式再解题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
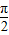 的奇函数
的奇函数 的偶函数
的偶函数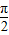 的奇函数
的奇函数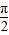 的偶函数
的偶函数