题目内容
是否存在常数a,b使等式 对于一切n∈N*都成立?若存在,求出a,b的值,若不存在,请说明理由。
对于一切n∈N*都成立?若存在,求出a,b的值,若不存在,请说明理由。
详见解析.
解析试题分析:先假设存在符合题意的常数a,b,c,再令n=1,n=2,n=3构造三个方程求出a,b,c,再用用数学归纳法证明成立,证明时先证:(1)当n=1时成立.(2)再假设n=k(k≥1)时,成立,递推到n=k+1时,成立即可.
试题解析:解:若存在常数a,b使得等式成立,将n=1,n=2代入等式
有:


即有: 4分
4分
对于n为所有正整数是否成立,再用数学归纳法证明
证明:(1)当n=1时,等式成立。 5分
(2)假设n=k时等式成立,即 7分
7分
当n=k+1时,即 11分
11分
也就是说n=k+1时,等式成立,
由(1)(2)可知等式对于任意的n∈N*都成立。 12分.
考点:数学归纳法.

练习册系列答案
相关题目
若复数z满足  ,则z的虚部为
,则z的虚部为
A. | B.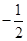 | C. | D. |
 ;
; ,试用分析法证明:
,试用分析法证明: .
. ;
; 均为实数,且
均为实数,且 ,
, ,
,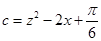 ,求证
,求证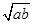 .
. ,那么x2+2x-1≠0.
,那么x2+2x-1≠0. 的前
的前 项组成集合
项组成集合 ,从集合
,从集合 中任取
中任取 个数,其所有可能的
个数,其所有可能的 个数的乘积的和为
个数的乘积的和为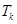 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
,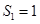 ;当
;当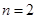 时,
时, ,
, ,
, .
. ;
;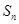 ,并用数学归纳法证明.
,并用数学归纳法证明.