题目内容
13.给出下列五个命题:①函数y=$\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$是偶函数,但不是奇函数;
②若lna<1成立,则a的取值范围是(-∞,e);
③函数f(x)=ax+1-2(a>0,a≠1)的图象过定点(-1,-1);
④方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0;
⑤函数f(x)=loga(6-ax)(a>0,a≠1)在[0,2]上为减函数,则1<a<3.
其中正确的个数( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 化简函数判断奇偶性说明①错误;求解对数不等式说明②错误;由指数函数的性质结合函数图象的平移说明③正确;由方程根的情况列关于a的不等式组求解a的范围说明④正确;利用复合函数的单调性求得a的范围说明⑤正确.
解答 解:①函数y=$\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$=0(x=±1),既是偶函数,又是奇函数,故①错误;
②若lna<1成立,则a的取值范围是(0,e),故②错误;
③∵y=ax的图象恒过(0,1),∴函数f(x)=ax+1-2(a>0,a≠1)的图象过定点(-1,-1),故③正确;
④方程x2+(a-3)x+a=0有一个正实根,一个负实根,则$\left\{\begin{array}{l}{(a-3)^{2}-4a>0}\\{a<0}\end{array}\right.$,即a<0,故④正确;
⑤∵a>0,a≠1,∴内函数t=6-ax为定义域上的减函数,要使函数f(x)=loga(6-ax)(a>0,a≠1)在[0,2]上为减函数,
则$\left\{\begin{array}{l}{a>1}\\{6-2a>0}\end{array}\right.$,即1<a<3,故⑤正确.
∴正确的命题个数是3个.
故选:C.
点评 本题考查命题的真假判断与应用,考查了函数的性质,⑤的解答技巧性较高,体现了对复合函数单调性的灵活运用,是中档题.

练习册系列答案
相关题目
1.已知全集U={1,2,3,4,5,6},集合A={1,3,5,6},则∁UA等于( )
| A. | {1,3,5} | B. | {2,4,6} | C. | {2,4} | D. | {1,3,5,6} |
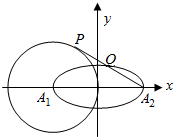 如图平面直角坐标系xOy中,椭圆$\frac{x^2}{4}+{y^2}=1$,A1,A2分别是椭圆的左、右两个顶点,圆A1的半径为2,过点A2作圆A1的切线,切点为P,在x轴的上方交椭圆于点Q.则$\frac{PQ}{Q{A}_{2}}$=$\frac{3}{4}$.
如图平面直角坐标系xOy中,椭圆$\frac{x^2}{4}+{y^2}=1$,A1,A2分别是椭圆的左、右两个顶点,圆A1的半径为2,过点A2作圆A1的切线,切点为P,在x轴的上方交椭圆于点Q.则$\frac{PQ}{Q{A}_{2}}$=$\frac{3}{4}$.