题目内容
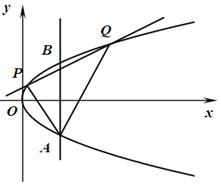
如图,两条相交线段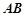 、
、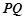 的四个端点都在抛物线
的四个端点都在抛物线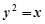 上,其中,直线
上,其中,直线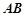 的方程为
的方程为 ,直线
,直线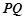 的方程为
的方程为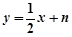 .
.
(1)若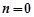 ,
,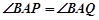 ,求
,求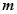 的值;
的值;
(2)探究:是否存在常数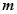 ,当
,当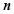 变化时,恒有
变化时,恒有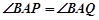 ?
?
(1) 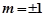 (2)
(2) 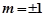
解析试题分析:
(1)联立直线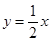 与抛物线方程可以求出
与抛物线方程可以求出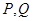 的坐标,设出A点的坐标,且满足A点在椭圆上和
的坐标,设出A点的坐标,且满足A点在椭圆上和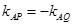 ,即根据AB为角平分线且与x轴垂直可得AP与AQ所在直线的倾斜角互为补角(斜率互为相反数),故两条件联立即可求出m的值.
,即根据AB为角平分线且与x轴垂直可得AP与AQ所在直线的倾斜角互为补角(斜率互为相反数),故两条件联立即可求出m的值.
(2) 联立直线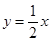 与椭圆方程得到关于
与椭圆方程得到关于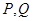 的坐标的韦达定理,由(1)这种特殊情况可得满足题意的只可能是
的坐标的韦达定理,由(1)这种特殊情况可得满足题意的只可能是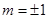 ,故一一带入验证是否能使得
,故一一带入验证是否能使得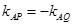 即可.
即可.
试题解析:
(1)由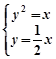 ,
,
解得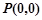 ,
,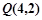 . 2分
. 2分
因为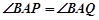 ,所以
,所以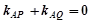 .
.
设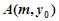 ,则
,则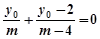 ,
,
化简得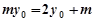 , 5分
, 5分
又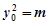 ,联立方程组,解得
,联立方程组,解得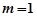 ,或
,或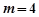 .
.
(也可以从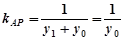 ,
,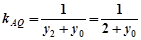 来解得)
来解得)
因为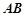 平分
平分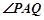 ,所以
,所以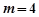 不合,故
不合,故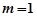 . 7分
. 7分
(2)设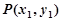 ,
, ,由
,由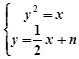 ,得
,得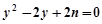 .
.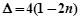 ,
,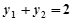 ,
,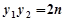 . 9分
. 9分
若存在常数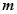 ,当
,当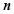 变化时,恒有
变化时,恒有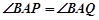 ,则由(Ⅰ)知只可能
,则由(Ⅰ)知只可能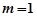 .
.
当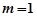 时,
时,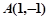 ,
,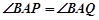 等价于
等价于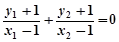 ,
,
即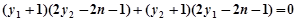 ,
,
即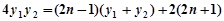 ,
,
即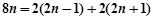 ,此式恒成立.
,此式恒成立.
(也可以从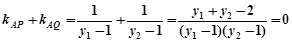 恒成立来说明)
恒成立来说明)
所以,存在常数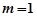 ,当
,当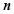 变化时,恒有
变化时,恒有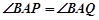 . 14分
. 14分
考点:斜率 抛物线

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 =1的离心率为2,焦点到渐近线的距离等于
=1的离心率为2,焦点到渐近线的距离等于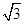 ,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.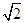 ,求直线l的方程.
,求直线l的方程. 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为 ;
; 到双曲线上动点
到双曲线上动点 的距离最小值为
的距离最小值为 .
. ,且
,且 .
. 的轨迹
的轨迹 的方程;
的方程; ,若斜率为
,若斜率为 的直线
的直线 过点
过点 并与轨迹
并与轨迹 ,且对于轨迹
,且对于轨迹 ,都存在
,都存在 ,使得
,使得 成立,试求出满足条件的实数
成立,试求出满足条件的实数 的值.
的值.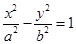
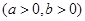 的左焦点
的左焦点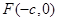
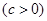 ,作倾斜角为
,作倾斜角为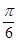 的直线
的直线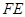 交该双曲线右支于点
交该双曲线右支于点 ,若
,若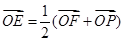 ,且
,且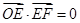 ,则双曲线的离心率为__________.
,则双曲线的离心率为__________. 直线
直线 与抛物线
与抛物线 没有交点;
没有交点; 方程
方程 表示椭圆;若
表示椭圆;若 为真命题,试求实数
为真命题,试求实数 的取值范围.
的取值范围.