题目内容
2.函数y=$\frac{1}{2}$x+cosx,x∈[0,2π]的单调减区间为($\frac{π}{6}$,$\frac{5π}{6}$).分析 设函数y=$\frac{1}{2}$x+cosx,求出导数y′,利用y′<0,求函数y的单调减区间.
解答 解:∵函数y=$\frac{1}{2}$x+cosx,
∴y′=$\frac{1}{2}$-sinx,
令y′<0,
解得sinx>$\frac{1}{2}$,
即$\frac{π}{6}$+2kπ<x<$\frac{5π}{6}$+2kπ,k∈Z;
当x∈[0,2π]时,函数y的单调减区间为($\frac{π}{6}$,$\frac{5π}{6}$).
故答案为:($\frac{π}{6}$,$\frac{5π}{6}$). (注:区间写开闭都对)
点评 本题考查了利用导数判断函数的单调性问题,也考查了三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
10.若函数f(x)=x3+2x2+mx+1在(-∞,+∞)内单调递增,则m的取值范围是( )
| A. | m$≥\frac{4}{3}$ | B. | m>$\frac{4}{3}$ | C. | m≤$\frac{4}{3}$ | D. | m$<\frac{4}{3}$ |
14.抛物线 x=-2y2的准线方程是( )
| A. | $y=\frac{1}{2}$ | B. | $y=\frac{1}{8}$ | C. | $x=\frac{1}{4}$ | D. | $x=\frac{1}{8}$ |
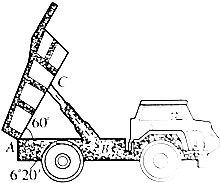 自动卸货汽车的车厢采用液压结构.设计时需要计算油泵顶杆BC的长度,已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20′,AC长为1.40m,计算BC的长(精确到0.01m).
自动卸货汽车的车厢采用液压结构.设计时需要计算油泵顶杆BC的长度,已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20′,AC长为1.40m,计算BC的长(精确到0.01m).