题目内容
当a<b<0时,比较 与
与 的大小.
的大小.
解:法一:利用“作差法”等价转化.
∵ -
- =
=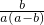 <0,
<0,
∴ <
< .
.
法二:利用“作商法”等价转化.
∵ =
= =1-
=1- <1,
<1,
且 <0,∴
<0,∴ >
> .
.
法三:利用不等式的性质等价转化.
∵a<b<0,∴a-b<0.又∵-b>0,∴a-b>a,
而(a-b)a>0,∴ >
> .
.
分析:本题可用三种方法进行比较,即法一:“作差法”利用同分化简后结果0比较;法二“做商法”变形后与1进行比较,法三利用等价变形后,利用不等式的性质进行判断大小关系.
点评:本题考查了比较大小的方法,可以用做商法或作差法、不等式的性质进行比较,难度不大,考查不等式的应用和一题多解的情况.
∵
 -
- =
=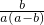 <0,
<0,∴
 <
< .
.法二:利用“作商法”等价转化.
∵
 =
= =1-
=1- <1,
<1,且
 <0,∴
<0,∴ >
> .
.法三:利用不等式的性质等价转化.
∵a<b<0,∴a-b<0.又∵-b>0,∴a-b>a,
而(a-b)a>0,∴
 >
> .
.分析:本题可用三种方法进行比较,即法一:“作差法”利用同分化简后结果0比较;法二“做商法”变形后与1进行比较,法三利用等价变形后,利用不等式的性质进行判断大小关系.
点评:本题考查了比较大小的方法,可以用做商法或作差法、不等式的性质进行比较,难度不大,考查不等式的应用和一题多解的情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
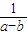 与
与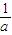 的大小.
的大小.