题目内容
设函数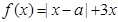 ,其中
,其中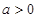 .
.
(1)当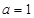 时,求不等式
时,求不等式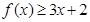 的解集;
的解集;
(2)若不等式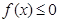 的解集为
的解集为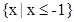 ,求
,求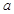 的值.
的值.
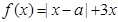 ,其中
,其中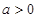 .
.(1)当
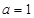 时,求不等式
时,求不等式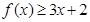 的解集;
的解集;(2)若不等式
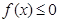 的解集为
的解集为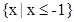 ,求
,求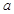 的值.
的值.(1) ,(2)
,(2)
 ,(2)
,(2)
试题分析:(1)解含绝对值不等式关键在于去掉绝对值,一般根据绝对值定义去绝对值,常需要分类讨论.本题化为形如
 或
或 ,最后结果要写出解集形式;(2)根据绝对值定义分类讨论去绝对值,
,最后结果要写出解集形式;(2)根据绝对值定义分类讨论去绝对值, 或
或 ,因为
,因为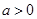 ,所以不等式的解集为
,所以不等式的解集为 ,比较已知条件
,比较已知条件 ,得
,得 ,故
,故 .本题也可从已知条件出发,去掉绝对值,因为
.本题也可从已知条件出发,去掉绝对值,因为 ,且
,且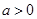 所以
所以 ,因而原不等式等价于
,因而原不等式等价于 ,即
,即 ,以下同前.
,以下同前.试题解析:
解:(1)当
 时,
时, 可化为
可化为 ,
,由此可得:
 ,
,故不等式的解集为
 4分
4分(2)由
 得
得
此不等式可化为不等式组
 或
或
即
 或
或 
因为
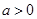 ,所以不等式的解集为
,所以不等式的解集为 8分
8分所以
 ,故
,故 。 10分
。 10分
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
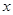 的不等式
的不等式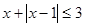 ;
; 有解,求实数
有解,求实数 的取值范围.
的取值范围.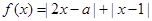 .
. 的解集;
的解集; 对
对 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. 的解集为( )
的解集为( )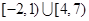



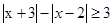 的解集为
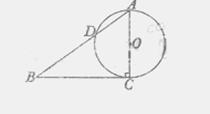
的解集为 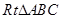 的两条直角边
的两条直角边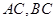 的长分别为3cm,4cm,以
的长分别为3cm,4cm,以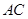 为直径的圆与
为直径的圆与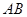 交于点
交于点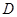 ,则
,则 .
.
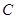 的参数方程为
的参数方程为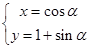 (
(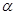 为参数)以原点为极点,
为参数)以原点为极点,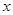 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线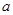 的极坐标方程为
的极坐标方程为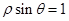 ,则直线
,则直线 .
.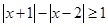 解集是_____________________.
解集是_____________________.