题目内容
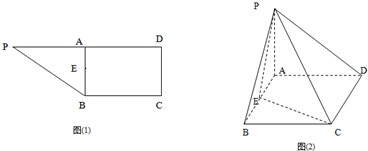
如图
=
.试探究EF、AD、BC之间的关系,并证明.
图
思路分析：首先从特例出发,如果=,取EB中点G,过G作GH∥BC,如图
图
则有H为FC的中点,
EF为梯形AGHD的中位线,
GH为梯形EBCF的中位线.∴EF=
(AD+GH),GH=
(EF+BC).
消去GH得3EF=BC+2AD.
同理,如果
=
,得5EF=2BC+3AD.
解:如果
,可以猜想(m+n)EF=mBC+nAD.
下面给出证明:
连结BD,交EF于G.
∵EG∥AD,∴
.∴EG=
AD.
又∵AD∥EF∥BC,∴
.
∵GF∥BC,∴
.∴GF=
BC.
∴EF=GF+EG=
BC+
AD.
∴(m+n)EF=mBC+nAD.
练习册系列答案
相关题目
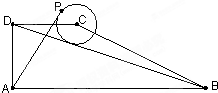如图；在直角梯形ABCD中，AB⊥AD，AD=DC=2，AB=6，动点P在以点C为圆心且与直线BD相切的圆上运动，设
如图，在等腰梯形ABCD中，AB=6，CD=4，梯形ABCD的面积是