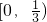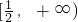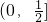题目内容
若在区间(-1,1)内任取实数a,在区间(0,1)内任取实数b,则直线ax-by=0与圆(x-1)2+(y-2)2=1相交的概率为分析:本题是一个等可能事件的概率,试验发生包含的事件是在区间(-1,1)内任取实数a,在区间(0,1)内任取实数b,对应的面积是2×1,满足条件的事件是圆心(1,2)到直线的距离小于或等于半径,整理出结果,得到概率.
解答:解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是在区间(-1,1)内任取实数a,在区间(0,1)内任取实数b,
对应的面积是2×1=2,
满足条件的事件是圆心(1,2)到直线的距离小于或等于半径,
即
≤1,
∴3b≥4a,
在所有事件组成的集合中,满足3b≥4a有x轴左边,b<1的部分,
∴要求的概率是
=
,
故答案为:
试验发生包含的事件是在区间(-1,1)内任取实数a,在区间(0,1)内任取实数b,
对应的面积是2×1=2,
满足条件的事件是圆心(1,2)到直线的距离小于或等于半径,
即
| |a-2b| | ||
|
∴3b≥4a,
在所有事件组成的集合中,满足3b≥4a有x轴左边,b<1的部分,
∴要求的概率是
1-
| ||||
| 2 |
| 5 |
| 16 |
故答案为:
| 5 |
| 16 |
点评:本题考查等可能事件的概率,要求得概率等于符合条件的面积之比,注意满足条件的事件所满足的条.件在整理时,应用点到直线的距离公式,注意变形整理.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
函数f(x)为偶函数,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是( )
A、[0,
| ||
B、[
| ||
C、[0,
| ||
D、(0,
|
若函数f(x)=3ax+1-2a在区间(-1,1)上存在一个零点,则a的取值范围是( )
A、a>
| ||
B、a>
| ||
C、-1<a<
| ||
| D、a<-1 |
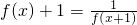 ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是