题目内容
设直线y=x+1与椭圆
+y2=1相交于A,B两点,则线段AB中点的坐标是
| x2 |
| 2 |
(-
,
)
| 2 |
| 3 |
| 1 |
| 3 |
(-
,
)
.| 2 |
| 3 |
| 1 |
| 3 |
分析:直接联立直线方程和椭圆方程,化为关于x的一元二次方程后利用根与系数关系得答案.
解答:解:设A(x1,y1),B(x2,y2),
联立
,得3x2+4x=0.
所以x1+x2=-
,则线段AB中点的横坐标为
=
=-
.
代入y=x+1得:y=-
+1=
.
所以线段AB中点的坐标是(-
,
).
故答案为(-
,
).
联立
|
所以x1+x2=-
| 4 |
| 3 |
| x1+x2 |
| 2 |
-
| ||
| 2 |
| 2 |
| 3 |
代入y=x+1得:y=-
| 2 |
| 3 |
| 1 |
| 3 |
所以线段AB中点的坐标是(-
| 2 |
| 3 |
| 1 |
| 3 |
故答案为(-
| 2 |
| 3 |
| 1 |
| 3 |
点评:本题考查了直线与圆锥曲线的关系,考查了“设而不求”的解题方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
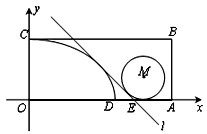 在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上(如图),且OC=1,OA=a+1(a>1),点D在边OA上,满足OD=a.分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD.直线l:y=-x+b与椭圆弧相切,与OA交于点E.
在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上(如图),且OC=1,OA=a+1(a>1),点D在边OA上,满足OD=a.分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD.直线l:y=-x+b与椭圆弧相切,与OA交于点E.
 +
+ =1(a>b>0)的焦点为F1,F2,P是椭圆上任意一点,若以坐标原点为圆心,椭圆短轴长为直径的圆经过椭圆的焦点,且△PF1F2的周长为4
=1(a>b>0)的焦点为F1,F2,P是椭圆上任意一点,若以坐标原点为圆心,椭圆短轴长为直径的圆经过椭圆的焦点,且△PF1F2的周长为4 .
. 上动点P(x,y)(x-y≠0)处的切线,l与椭圆C交于不同的两点Q,R,证明:∠QOR的大小为定值.
上动点P(x,y)(x-y≠0)处的切线,l与椭圆C交于不同的两点Q,R,证明:∠QOR的大小为定值.
