题目内容
已函数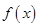 是定义在
是定义在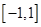 上的奇函数,在
上的奇函数,在 上
上 .
.
(1)求函数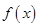 的解析式;并判断
的解析式;并判断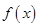 在
在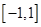 上的单调性(不要求证明);
上的单调性(不要求证明);
(2)解不等式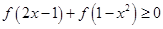 .
.
(1)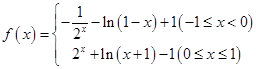 ;(2)
;(2)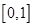 .
.
解析试题分析:{设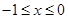 ,则
,则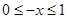 }是求函数解析式问题的重要方法,即求那个区间的解析式设自变量在那个区间,然后运用奇函数的性质进行转化;注意运用{在相同定义域内,增
}是求函数解析式问题的重要方法,即求那个区间的解析式设自变量在那个区间,然后运用奇函数的性质进行转化;注意运用{在相同定义域内,增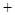 增
增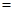 增; 减
增; 减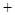 减
减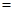 减}判断函数的单调性.(2)利用函数的单调性解不等式,同时注意函数的定义域.
减}判断函数的单调性.(2)利用函数的单调性解不等式,同时注意函数的定义域.
试题解析:(1)设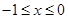 ,则
,则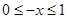
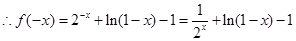
又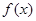 是奇函数,所以
是奇函数,所以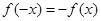 ,
,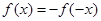 =
=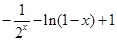 3分
3分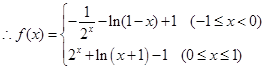
4分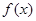 是[-1,1]上增函数 .6分
是[-1,1]上增函数 .6分
(2)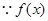 是[-1,1]上增函数,由已知得:
是[-1,1]上增函数,由已知得: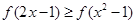 .7分
.7分
等价于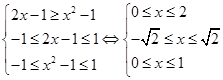 ...10分
...10分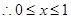
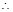 不等式的解集为
不等式的解集为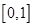 12分
12分
考点:求函数解析式,函数的单调性,函数的奇偶性,解不等式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
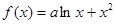 (
(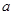 为实常数)
为实常数) 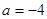 时,求函数
时,求函数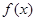 在
在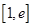 上的最大值及相应的
上的最大值及相应的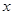 值;
值;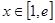 时,讨论方程
时,讨论方程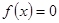 根的个数
根的个数 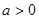 ,且对任意的
,且对任意的 ,都有
,都有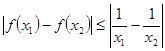 ,求实数a的取值范围
,求实数a的取值范围 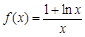 .
.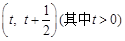 上存在极值,求实数
上存在极值,求实数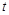 的取值范围;
的取值范围;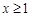 时,不等式
时,不等式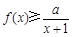 恒成立,求实数
恒成立,求实数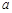 的取值范围.
的取值范围.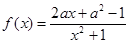 ,其中
,其中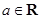 .
.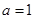 时,记
时,记 存在
存在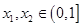 使
使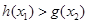 成立,求实数
成立,求实数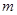 的取值范围;
的取值范围;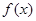 在
在 上存在最大值和最小值,求
上存在最大值和最小值,求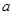 的取值范围.
的取值范围.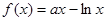 ,
,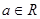
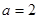 时,求曲线
时,求曲线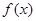 在点
在点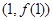 处的切线方程;
处的切线方程;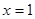 处有极值,求
处有极值,求 ,使
,使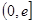 的最小值是3,若存在,求出
的最小值是3,若存在,求出 是
是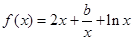 的一个极值点.
的一个极值点.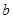 的值;
的值; 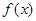 的单调递减区间;
的单调递减区间; ,试问过点
,试问过点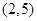 可作多少条直线与曲线
可作多少条直线与曲线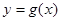 相切?请说明理由.
相切?请说明理由. 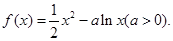
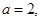 求
求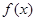 在
在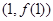 处的切线方程;
处的切线方程;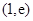 上恰有两个零点,求
上恰有两个零点,求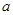 的取值范围.
的取值范围.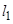 排,在路南侧沿直线
排,在路南侧沿直线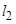 排,现要在矩形区域
排,现要在矩形区域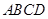 内沿直线将
内沿直线将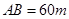 ,
,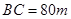 ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的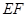 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设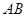 所成的小于
所成的小于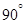 的角为
的角为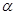 .
.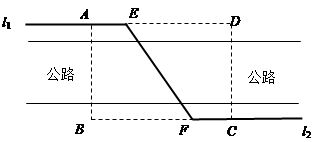
 关于
关于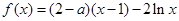 ,
,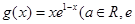 为自然对数的底数).
为自然对数的底数).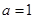 时,求
时,求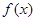 的单调区间;
的单调区间;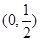 上无零点,求
上无零点,求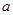 最小值;
最小值; ,在
,在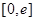 上总存在两个不同的
上总存在两个不同的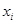
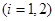 ),使
),使 成立,求
成立,求