题目内容
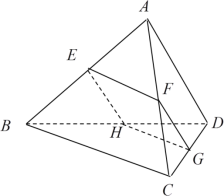
【题目】如图所示,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG. 
(1)求证:AC是∠DAB的平分线;
(2)求证:OF∥AG.
【答案】
(1)解:∵CF=FG
∴∠CGF=∠FCG
∴AB圆O的直径
∴∠ACB=∠ADB=90°
∵CE⊥AB
∴∠CEA=90°
∵∠CBA=90°﹣∠CAB,∠ACE=90°﹣∠CAB
∴∠CBA=∠ACE
∵∠CGF=∠DGA,
∴∠DGA=∠ABC
∴∴∠CAB=∠DAC
∴C为劣弧BD的中点,
∴AC是∠DAB的平分线;
(2)解:∵∠GBC=90°﹣∠CGB,∠FCB=90°﹣∠GCF
∴∠GBC=∠FCB
∴CF=FB
同理可证:CF=GF
∴BF=FG,
∵OA=OB,
∴OF∥AG.
【解析】(1)要证明C是劣弧BD的中点,即证明弧BC与弧CD相等,即证明∠CAB=∠DAC,根据已知中CF=FG,AB是圆O的直径,CE⊥AB于E,我们易根据同角的余角相等,得到结论.(2)由已知及(I)的结论,我们易证明△BFC及△GFC均为等腰三角形,即CF=BF,CF=GF,进而得到结论.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目