[题目]如图.三棱柱A1B1C1-ABC中.侧棱AA1⊥底面ABC.底面三角形ABC是正三角形.E是BC中点.则下列叙述正确的是( )A.AC⊥平面ABB1A1B.CC1与B1E是异面直线C.A1C1∥B1ED.AE⊥BB1 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，三棱柱A1B1C1-ABC中，侧棱AA1⊥底面ABC，底面三角形ABC是正三角形，E是BC中点，则下列叙述正确的是（）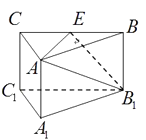

A.AC⊥平面ABB1A1
B.CC1与B1E是异面直线
C.A1C1∥B1E
D.AE⊥BB1

【答案】D
【解析】因为三棱柱A1B1C1-ABC中,侧棱AA1⊥底面ABC，底面三角形ABC是正三角形，E是BC中点，

所以对于A,AC与AB夹角为60°,即两直线不垂直，所以. AC不可能垂直于平面ABB1A1；故A错误；

对于B,CC1与B1E都在平面CC1BB1中不平行，故相交；所以B错误；

对于C,A1C1,B1E是异面直线；故C错误；

对于D,因为几何体是三棱柱,并且侧棱AA1⊥底面ABC，底面三角形ABC是正三角形，E是BC中点，所以BB1⊥底面ABC,所以BB1⊥AE,AE⊥BC,得到AE⊥平面BCC1B1,所以AE⊥BB1；

所以答案是：D.

【考点精析】关于本题考查的空间中直线与直线之间的位置关系和空间中直线与平面之间的位置关系，需要了解相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线：不同在任何一个平面内，没有公共点；直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点才能得出正确答案．

练习册系列答案

【题目】随机抽取某班6名学生，测量他们的身高（单位：cm），获得身高数据依次为：162，168，170，171，179，182，那么此班学生平均身高大约为cm；样本数据的方差为．

【题目】已知曲线C：f（x）=x3﹣ax+a，若过曲线C外一点A（1，0）引曲线C的两条切线，它们的倾斜角互补，则a的值为．

【题目】某校在“普及环保知识节”后，为了进一步增强环保意识，从本校学生中随机抽取了一批学生参加环保基础知识测试．经统计，这批学生测试的分数全部介于75至100之间．将数据分成以下5组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到如图所示的频率分布直方图．
（Ⅰ）求a的值；
（Ⅱ）现采用分层抽样的方法，从第3，4，5组中随机抽取6名学生座谈，求每组抽取的学生人数；
（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替，试估计随机抽取学生所得测试分数的平均值在第几组（只需写出结论）．

【题目】已知△ABC的顶点B（-1，-3），边AB上的高CE所在直线的方程为，BC边上中线AD所在的直线方程为．
（1）求直线AB的方程；
（2）求点C的坐标．

【题目】函数f（x）= 的定义域是（）
A.{x|x≥4}
B.{x|x＜4}
C.{x|x≤4，且x≠1}
D.{x|x＜4，且x≠﹣1}

【题目】某公司生产三种型号的轿车，产量分别是1600辆、6000辆和2000辆，为检验公司的产品质量，现从这三种型号的轿车种抽取48辆进行检验，这三种型号的轿车依次应抽取．

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC= AD=1，CD= ．

（1）求证：平面PQB⊥平面PAD；
（2）若二面角M﹣QB﹣C为30°，求线段PM与线段MC的比值t．

试题分类