题目内容
设函数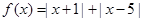 ,
,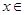
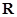 .
.
⑴ 求不等式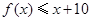 的解集;
的解集;
⑵ 如果关于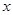 的不等式
的不等式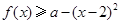 在
在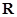 上恒成立,求实数
上恒成立,求实数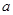 的取值范围.
的取值范围.
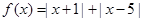 ,
,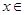
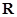 .
.⑴ 求不等式
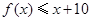 的解集;
的解集;⑵ 如果关于
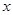 的不等式
的不等式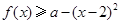 在
在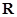 上恒成立,求实数
上恒成立,求实数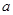 的取值范围.
的取值范围.(1)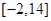 (2)
(2)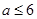
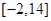 (2)
(2)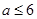
试题分析:(1)利用分类讨论思想去掉绝对值,得到分段函数,逐一求解;(2)构造函数
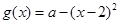 采用数形结合思想,借助两个函数图象进行比较分析.
采用数形结合思想,借助两个函数图象进行比较分析.试题解析:(1)
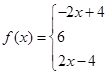
 (2分)
(2分)当
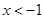 时,
时,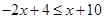 ,
,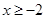 ,则
,则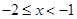 ;
;当
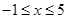 时,
时,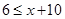 ,
, ,则
,则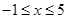 ;
;当
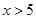 时,
时,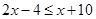 ,
,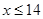 ,则
,则 .
.综上可得,不等式的解集为
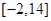 . (5分)
. (5分)(2) 设
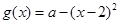 ,由函数
,由函数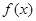 的图像与
的图像与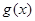 的图像可知:
的图像可知: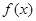 在
在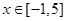 时取最小值为6,
时取最小值为6,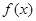 在
在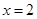 时取最大值为
时取最大值为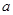 ,
,若
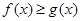 恒成立,则
恒成立,则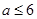 . (10分)
. (10分)
练习册系列答案
相关题目
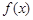 是定义在
是定义在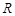 上的奇函数,且当
上的奇函数,且当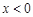 时,
时,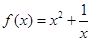 .
.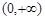 上的单调性.
上的单调性.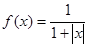 的图象是 ( )
的图象是 ( ) 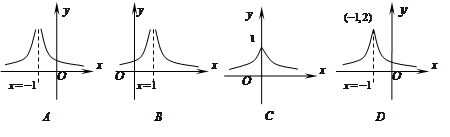
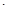 g(x)是偶函数
g(x)是偶函数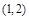 内是增函数的为( )
内是增函数的为( )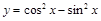
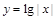
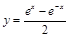
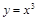
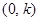 (其中
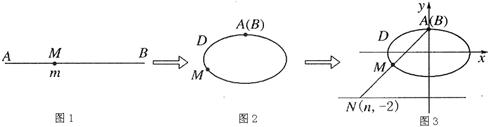
(其中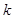 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间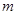 对应线段
对应线段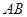 上的点
上的点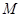 ,如图1;将线段
,如图1;将线段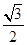 的椭圆,使两端点
的椭圆,使两端点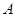 、
、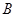 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在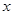 轴上,已知此时点
轴上,已知此时点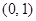 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段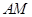 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线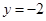 交于点
交于点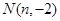 ,则与实数
,则与实数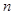 ,记作
,记作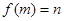 ,
,
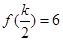 ; ②函数
; ②函数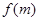 是奇函数;③函数
是奇函数;③函数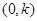 上单调递增; ④.函数
上单调递增; ④.函数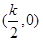 对称;⑤函数
对称;⑤函数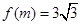 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )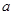 为实常数,
为实常数,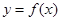 是定义在R上的奇函数,当
是定义在R上的奇函数,当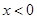 时,
时,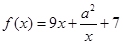 ,若
,若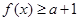 对一切
对一切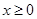 成立,则
成立,则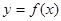 是奇函数,如果
是奇函数,如果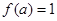 ,那么
,那么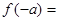 _______
_______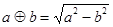 ,
,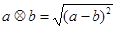 ,则函数
,则函数 为( )
为( )