题目内容
已知点P在以坐标轴为对称轴的椭圆上,且P到两焦点的距离分别为5、3,过P且与长轴垂直的直线恰过椭圆的一个焦点,求椭圆的方程.
【答案】分析:先假设出椭圆的标准形式,再由P到两焦点的距离分别为5、3得到2a=5+3得到a的值,结合过P且与长轴垂直的直线恰过椭圆的一个焦点,可求得c的值,进而可求得椭圆的方程.
解答:解:设所求的椭圆方程为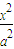 +
+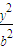 =1(a>b>0)或
=1(a>b>0)或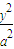 +
+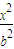 =1(a>b>0),
=1(a>b>0),
由已知条件得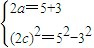 ,
,
a=4,c=2,b2=12.
故所求方程为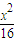 +
+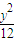 =1或
=1或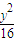 +
+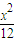 =1.
=1.
点评:本题主要考查椭圆的基本性质的运用.椭圆的基本性质是高考的重点内容,一定要熟练掌握并能够灵活运用.
解答:解:设所求的椭圆方程为
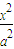 +
+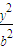 =1(a>b>0)或
=1(a>b>0)或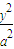 +
+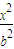 =1(a>b>0),
=1(a>b>0),由已知条件得
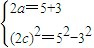 ,
,a=4,c=2,b2=12.
故所求方程为
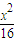 +
+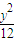 =1或
=1或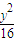 +
+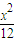 =1.
=1.点评:本题主要考查椭圆的基本性质的运用.椭圆的基本性质是高考的重点内容,一定要熟练掌握并能够灵活运用.

练习册系列答案
相关题目
 和
和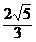 ,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程.
,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程.