题目内容
已知点P 在以坐标轴为对称轴的椭圆上,点P 到两个焦点的距离分别为 和
和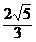 ,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程.
,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程.
 和
和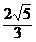 ,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程.
,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程.解:设两焦点为F1 ,F2 ,
有|PF1|=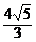 ,|PF2|=
,|PF2|=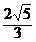 ,
,
由椭圆的定义知2a=|PF1|+|PF2|=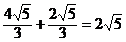
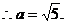
∵|PF1|>|PF2|.
∴由题意知△PF1F2为直角三角形,
在△PF1F2中,sin∠PF1F2=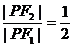
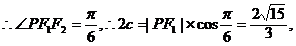

∴b2=a2-c2=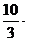
∵焦点可以在x轴上,也可以在y轴上.
∴椭圆的方程为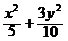 或
或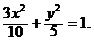
有|PF1|=
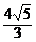 ,|PF2|=
,|PF2|=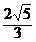 ,
,由椭圆的定义知2a=|PF1|+|PF2|=
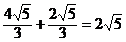
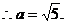
∵|PF1|>|PF2|.
∴由题意知△PF1F2为直角三角形,
在△PF1F2中,sin∠PF1F2=
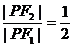
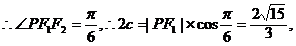

∴b2=a2-c2=
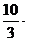
∵焦点可以在x轴上,也可以在y轴上.
∴椭圆的方程为
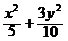 或
或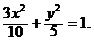

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目