题目内容
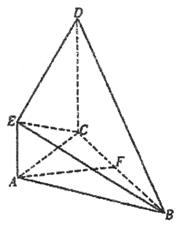
（本小题满分12分）如图所示，直角梯形ACDE与等腰直角△ABC所在平面互相垂直，F为BC的中点，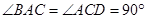
，AE∥CD，DC=AC=2AE=2.
（Ⅰ）求证：平面BCD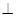
平面ABC
（Ⅱ）求证：AF∥平面BDE；
（Ⅲ）求四面体B-CDE的体积.
【答案】
（本小题满分12分）
解：（Ⅰ）∵面ABC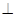
面ACDE，面ABC
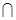面ACDE=AC，CD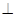AC，
∴DC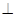面ABC，………………………………………………2分
又∵DC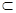
面BCD，∴平面BCD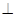平面ABC. ………………4分
（Ⅱ）取BD的中点P，连结EP、FP，则PF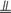 
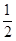DC,
又∵EA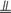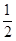DC，∴EA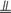PF，……………………………6分
∴四边形AFPE是平行四边形，∴AF∥EP，
又∵EP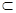面BDE，∴AF∥面BDE.…………………8分
（Ⅲ）∵BA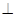AC，面ABC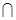面ACDE=AC，∴BA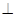面ACDE.
∴BA就是四面体B-CDE的高，且BA=2. ……………10分
∵DC=AC=2AE=2，AE∥CD，
∴
∴
∴
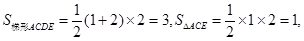
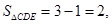
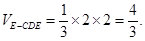……………………………………12分
【解析】略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
