题目内容
已知函数f(x)=(sinωx-cosωx)2+2sin2ωx(ω>0)的周期为 .
.
(Ⅰ) 求函数y=f(x)在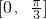 上的值域;
上的值域;
(Ⅱ)求最小的正实数?,使得y=f(x)的函数图象向右平移?个单位后所对应的函数为偶函数.
解:f(x)=(sinωx-cosωx)2+2sin2ωx=1-2sinωxcosωx+(1-cos2ωx)
=2-sin2ωx-cos2ωx=2- sin(2ωx+
sin(2ωx+ )
)
由T= ,得到|ω|=
,得到|ω|= ,又ω>0,
,又ω>0,
∴ω= ,
,
则f(x)=2- sin(3x+
sin(3x+ ),
),
(Ⅰ)由
则函数y=f(x)在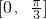 上的值域为
上的值域为 ;
;
(Ⅱ)∵y=f(x)的函数图象向右平移?个单位后所对应的函数为:
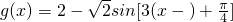
则y=g(x)为偶函数,则有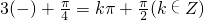
则φ=- π-
π- (k∈Z),又因为φ>0,
(k∈Z),又因为φ>0,
∴满足条件的最小正实数φ= .
.
分析:把f(x)的解析式先利用完全平方公式及二倍角的余弦函数公式化简,再根据同角三角函数间的基本关系及两角和与差的正弦函数公式化为一个角的正弦函数,根据已知的周期,利用周期公式求出ω的值,从而确定出函数f(x)的解析式,
(Ⅰ)由函数定义域x的范围,求出f(x)中正弦函数角的范围,根据正弦函数的图象与性质,即可得到f(x)的值域;
(Ⅱ)先根据平移规律:左加右减,表示出f(x)的函数图象向右平移?个单位后所对应的函数g(x),然后根据g(x)为偶函数,根据偶函数的定义g(-x)=g(x),即可表示出φ,再根据φ>0,得到满足题意的最小正实数φ的值.
点评:此题考查了同角三角函数间的基本关系,二倍角的正弦、余弦函数公式,以及两角和与差的正弦函数公式,同时考查了正弦函数的图象与性质,平移规律以及偶函数的定义,其中灵活运用三角函数的恒等变形把已知函数化为一个角的正弦函数,进而利用周期公式求出ω的值,确定出f(x)的解析式是本题的突破点.
=2-sin2ωx-cos2ωx=2-
 sin(2ωx+
sin(2ωx+ )
)由T=
 ,得到|ω|=
,得到|ω|= ,又ω>0,
,又ω>0,∴ω=
 ,
,则f(x)=2-
 sin(3x+
sin(3x+ ),
),(Ⅰ)由

则函数y=f(x)在
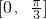 上的值域为
上的值域为 ;
;(Ⅱ)∵y=f(x)的函数图象向右平移?个单位后所对应的函数为:
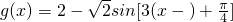
则y=g(x)为偶函数,则有
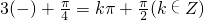
则φ=-
 π-
π- (k∈Z),又因为φ>0,
(k∈Z),又因为φ>0,∴满足条件的最小正实数φ=
 .
.分析:把f(x)的解析式先利用完全平方公式及二倍角的余弦函数公式化简,再根据同角三角函数间的基本关系及两角和与差的正弦函数公式化为一个角的正弦函数,根据已知的周期,利用周期公式求出ω的值,从而确定出函数f(x)的解析式,
(Ⅰ)由函数定义域x的范围,求出f(x)中正弦函数角的范围,根据正弦函数的图象与性质,即可得到f(x)的值域;
(Ⅱ)先根据平移规律:左加右减,表示出f(x)的函数图象向右平移?个单位后所对应的函数g(x),然后根据g(x)为偶函数,根据偶函数的定义g(-x)=g(x),即可表示出φ,再根据φ>0,得到满足题意的最小正实数φ的值.
点评:此题考查了同角三角函数间的基本关系,二倍角的正弦、余弦函数公式,以及两角和与差的正弦函数公式,同时考查了正弦函数的图象与性质,平移规律以及偶函数的定义,其中灵活运用三角函数的恒等变形把已知函数化为一个角的正弦函数,进而利用周期公式求出ω的值,确定出f(x)的解析式是本题的突破点.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|