题目内容
（本小题满分12分，（Ⅰ）小问5分，（Ⅱ）小问7分.）
如题（21）图，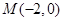
和
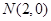的平面上的两点，动点
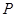满足：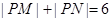
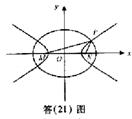
（Ⅰ）求点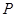的轨迹方程；
（Ⅱ）若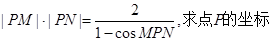
。
【答案】
（Ⅰ）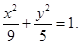
（Ⅱ）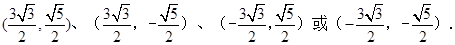
【解析】(Ⅰ)由椭圆的定义，点P的轨迹是以M、N为焦点，长轴长2a=6的椭圆.
因此半焦距c=2，长半轴a=3，从而短半轴
b=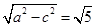
，
所以椭圆的方程为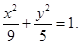
(Ⅱ)由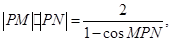
得
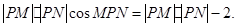①
因为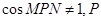
不为椭圆长轴顶点，故P、M、N构成三角形.在△PMN中，
②
将①代入②，得
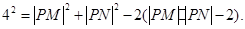
故点P在以M、N为焦点，实轴长为
的双曲线
上.
由(Ⅰ)知，点P的坐标又满足
，所以
由方程组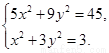
解得
即P点坐标为
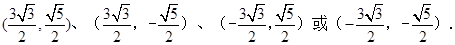
练习册系列答案
津桥教育计算小状元系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
