题目内容
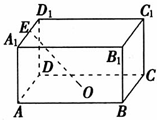 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1.设点P的轨迹为L,则L的离心率等于
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1.设点P的轨迹为L,则L的离心率等于
| ||
| 2 |
| ||
| 2 |
分析:由题意可知点P在以OE为轴,半径为1的圆柱侧面上,点P又在底面ABCD上,得点P的轨迹是平面ABCD与圆柱侧面的交线,想象知其必为椭圆,由轴OE与ABCD成45°,可算得其离心率
解答:解:由题意可知:知点P的轨迹为椭圆,作EF⊥AD于点F,则EF=OF=2,△OEF为等腰直角三角形,得轴OE与平面ABCD所成的角为45°,
∵P的轨迹是椭圆,而半长轴长a=
,短半轴长为b=1,
∴c2=a2-b2=1,
∴e=
=
.
故答案为:
∵P的轨迹是椭圆,而半长轴长a=
| 2 |
∴c2=a2-b2=1,
∴e=
| 1 | ||
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查立体几何与椭圆的交汇,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.