题目内容
 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.(1)求三棱锥A-MCC1的体积;
(2)当M为中点时,求证:B1M⊥平面MAC.
分析:(1)由图形直接求出三棱锥的底面积和高,代入体积公式加以计算,即可得到三棱锥A-MCC1的体积;
(2)利用勾股定理,算出B1D1=
,从而得到B1M=
,同理得到B1C=
且CM=
,△B1CM中利用勾股定理的逆定理证出B1M⊥MC.同理证出B1M⊥AM,再利用线面垂直的判定定理即可证出B1M⊥平面MAC.
(2)利用勾股定理,算出B1D1=
| 2 |
| 3 |
| 5 |
| 2 |
解答: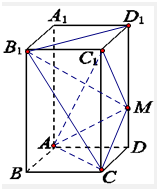 解:(1)根据题意,可得
解:(1)根据题意,可得
AD⊥平面MCC1,即AD=1是三棱锥A-MCC1的高
∵S△ MCC1=
SCC1D1D=
×1×2=1
∴三棱锥A-MCC1的体积V=
S△ MCC1•AD=
×1×1=
;
(2)正方形A1B1C1D1中,B1D1=
=
Rt△B1D1M中,D1M=
D1D=1,∴B1M=
=
同理可得B1C=
,CM=
∴△B1CM中,B1C2=CM2+B1M2,可得∠B1MC=90°,即B1M⊥MC
同理可得B1M⊥AM
∵AM、MC是平面MAC内的相交直线,
∴B1M⊥平面MAC.
 解:(1)根据题意,可得
解:(1)根据题意,可得AD⊥平面MCC1,即AD=1是三棱锥A-MCC1的高
∵S△ MCC1=
| 1 |
| 2 |
| 1 |
| 2 |
∴三棱锥A-MCC1的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)正方形A1B1C1D1中,B1D1=
| A1B12+A 1D12 |
| 2 |
Rt△B1D1M中,D1M=
| 1 |
| 2 |
| D1M2+B 1D12 |
| 3 |
同理可得B1C=
| 5 |
| 2 |
∴△B1CM中,B1C2=CM2+B1M2,可得∠B1MC=90°,即B1M⊥MC
同理可得B1M⊥AM
∵AM、MC是平面MAC内的相交直线,
∴B1M⊥平面MAC.
点评:本题在正四棱柱中证明线面垂直,并求三棱锥的体积.着重考查了线面垂直的判定与性质、勾股定理及其逆定理和正四棱柱的性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目