题目内容
已知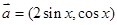 ,
,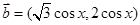 ,且
,且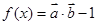 .
.
(1)求函数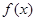 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(2)若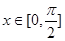 ,求函数
,求函数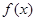 的最大值与最小值.
的最大值与最小值.
(1) ,函数
,函数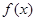 的单调增区间为
的单调增区间为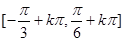
(2)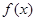 的最大值为
的最大值为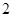 ,
,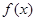 的最小值为
的最小值为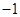
解析试题分析:(1)因为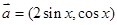 ,
,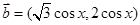 ,所以
,所以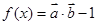 =2
=2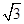 sinxcosx+2cos2x-1=
sinxcosx+2cos2x-1=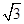 sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+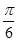 ).所以f(x)的最小正周期为T=
).所以f(x)的最小正周期为T= =π,由2kπ-
=π,由2kπ- ≤2x+
≤2x+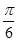 ≤2kπ+
≤2kπ+ ,k∈Z解得kπ-
,k∈Z解得kπ-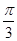 ≤x≤kπ+
≤x≤kπ+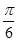 ,即单调递增区间为
,即单调递增区间为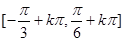
(2)由(1)可知f(x)在区间[0,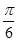 ]上单调递增,在[
]上单调递增,在[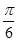 ,
, ]上单调递减,故当x=
]上单调递减,故当x=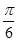 时,f(x)取到最大值f(
时,f(x)取到最大值f(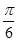 )=2;当x=
)=2;当x= 时,f(x)取到最大值f(
时,f(x)取到最大值f( )=-1.
)=-1.
考点:本题考查了数量积的坐标运算及三角函数的性质
点评:本题为三角函数与向量的综合应用,准确记住公式是解决问题的关键,属中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
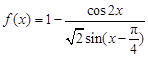 .
. 的定义域;
的定义域;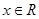 ,
,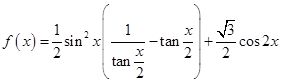 .
.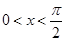 ,求
,求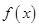 的单调的递减区间;
的单调的递减区间;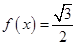 ,求
,求 的值.
的值.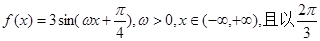 为最小正周期.
为最小正周期.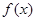 的解析式;
的解析式;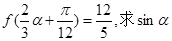 的值.
的值. 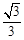 .
.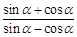 的值.
的值.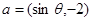 与
与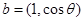 互相垂直,其中
互相垂直,其中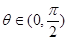
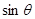 和
和 的值
的值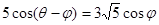 ,
,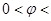
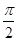 ,求
,求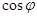 的值
的值 .
.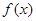 的最小值和最小正周期;
的最小值和最小正周期;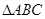 内角
内角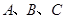 的对边分别为
的对边分别为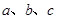 ,且
,且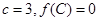 ,
,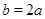 ,求
,求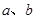 的值.
的值.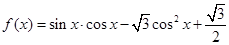 .
. 的对称轴方程和单调递增区间;
的对称轴方程和单调递增区间;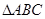 中,
中,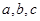 分别是角
分别是角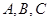 的对边,且
的对边,且 ,
,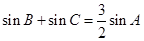 ,求
,求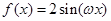 ,其中常数
,其中常数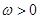 ;
; 在
在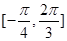 上单调递增,求
上单调递增,求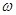 的取值范围;
的取值范围;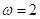 ,将函数
,将函数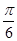 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数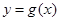 的图像,区间
的图像,区间 (
(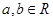 且
且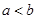 )满足:
)满足: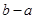 的最小值.
的最小值.