题目内容
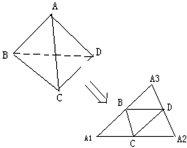 已知四面体ABCD,沿棱AB、AC、AD剪开,铺成平面图形,得到△A1A2A3(如图),试写出四面体ABCD应满足的一个性质:________.
已知四面体ABCD,沿棱AB、AC、AD剪开,铺成平面图形,得到△A1A2A3(如图),试写出四面体ABCD应满足的一个性质:________.
四面体是正四面体;或者四面体的三个角B,C,D处的三个角的和都是180°
分析:仔细观察,发现展开后的图形是三角形,A1,A2,A3,三点与A重合,只要满足题意的一个性质即可.
解答:仔细观察,发现四面体ABCD,沿棱AB、AC、AD剪开,铺成平面图形,展开后的图形是三角形,A1,A2,A3,三点与A重合,不妨四面体是正四面体即可满足题意.
故答案为:四面体是正四面体;或者四面体的三个角B,C,D处的三个角的和都是180°.
点评:本题是中档题,考查几何体的折叠与展开,注意这两科后的图形的特征是解题的关键,同时注意到特殊图形的应用.
分析:仔细观察,发现展开后的图形是三角形,A1,A2,A3,三点与A重合,只要满足题意的一个性质即可.
解答:仔细观察,发现四面体ABCD,沿棱AB、AC、AD剪开,铺成平面图形,展开后的图形是三角形,A1,A2,A3,三点与A重合,不妨四面体是正四面体即可满足题意.
故答案为:四面体是正四面体;或者四面体的三个角B,C,D处的三个角的和都是180°.
点评:本题是中档题,考查几何体的折叠与展开,注意这两科后的图形的特征是解题的关键,同时注意到特殊图形的应用.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知四面体ABCD中,AB=AD=6,AC=4,CD=2
,AB⊥平面ACD,则四面体ABCD外接球的表面积为( )
| 13 |
| A、36π | B、88π |
| C、92π | D、128π |
 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3 已知四面体ABCD中,
已知四面体ABCD中,