题目内容
已知四面体ABCD(图1),沿AB、AC、AD剪开,展成的平面图形正好是图2所示的直角梯形A1A2A3D(梯形的顶点A1、A2、A3重合于四面体的顶点A).(1)证明:AB⊥CD.
(2)当A1D=10,A1A2=8时,求四面体ABCD的体积.
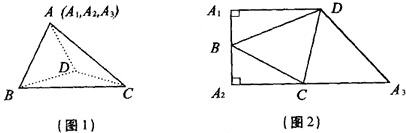
分析:(1)要证AB⊥CD,先证AB⊥面ACD,在其展成的平面图形中A1B⊥A1D,A2B⊥A2C,从而AB⊥AC,AB⊥AD,可得线面垂直,即可得线线垂直.
(2)要求四面体ABCD的体积,先确定其底面和高线,然后分别求其值,利用三棱锥的体积公式,即可得其体积.
(2)要求四面体ABCD的体积,先确定其底面和高线,然后分别求其值,利用三棱锥的体积公式,即可得其体积.
解答:解:
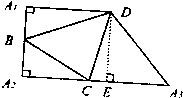 (I)证明:由图2,A1A2A3D为直角梯形,
(I)证明:由图2,A1A2A3D为直角梯形,
得A1B⊥A1D,A2B⊥A2C.
即图1中,AB⊥AC,AB⊥AD.
又AC∩AD=A,∴AB⊥面ACD.
∵CD?面ACD,∴AB⊥CD.
(II)在图2中,作DE⊥A2A3于E,
∵A1A2=8,∴DE=8,
又∵A1D=A3D=10,∴EA3=6,∴A2A3=10+6=16.
而A2C=A3C,∴A2C=8,即图1中AC=8,AD=10.
由A1A2=8,A1B=A2B,得图1中AB=4.
S△ACD=S△A3CD=
×8×8=32.
由(I)知,AB⊥面ACD,∴VB-ACD=
×32×4=
.
 (I)证明:由图2,A1A2A3D为直角梯形,
(I)证明:由图2,A1A2A3D为直角梯形,得A1B⊥A1D,A2B⊥A2C.
即图1中,AB⊥AC,AB⊥AD.
又AC∩AD=A,∴AB⊥面ACD.
∵CD?面ACD,∴AB⊥CD.
(II)在图2中,作DE⊥A2A3于E,
∵A1A2=8,∴DE=8,
又∵A1D=A3D=10,∴EA3=6,∴A2A3=10+6=16.
而A2C=A3C,∴A2C=8,即图1中AC=8,AD=10.
由A1A2=8,A1B=A2B,得图1中AB=4.
S△ACD=S△A3CD=
| 1 |
| 2 |
由(I)知,AB⊥面ACD,∴VB-ACD=
| 1 |
| 3 |
| 128 |
| 3 |
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,注意辅助线的作法,是个中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知四面体ABCD中,AB=AD=6,AC=4,CD=2
,AB⊥平面ACD,则四面体ABCD外接球的表面积为( )
| 13 |
| A、36π | B、88π |
| C、92π | D、128π |
 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3 已知四面体ABCD中,
已知四面体ABCD中,