题目内容
【题目】如图,焦点在x轴的椭圆,离心率e= ![]() ,且过点A(﹣2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点(Q点与P点不重合).
,且过点A(﹣2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点(Q点与P点不重合).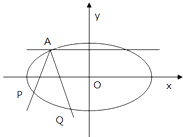
(1)求椭圆标准方程;
(2)求证:直线PQ的斜率为定值;
(3)求△OPQ的面积的最大值.
【答案】
(1)解:设椭圆方程为 ![]() ,
,
∵椭圆经过点(﹣2,1),
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴椭圆方程为 ![]()
(2)证明:设直线AP方程为y=k(x+2)+1,则直线AQ的方程为y=﹣k(x+2)+1
由 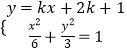 可得(1+2k2)x2+4k(2k+1)x+8k2+8k﹣4=0,△>0,
可得(1+2k2)x2+4k(2k+1)x+8k2+8k﹣4=0,△>0,
设P(x1,y1),由A(﹣2,1)可得 ![]() ,
,
∴P( ![]() ,
, ![]() ),
),
同理可得Q( ![]() ,
, ![]() ),
),
∴kPQ=﹣1
(3)由(2),设PQ的方程为y=﹣x+m,代入椭圆方程得:3x2﹣4mx+2m2﹣6=0.
令△>0,得﹣3<m<3,
设P(x1,y1),Q(x2,y2),则 ![]() ,
,
∴ ![]()
设原点O到直线的距离为d,则 ![]() ,
,
∴ ![]() ,
,
当 ![]() 时,△OPQ面积的最大值为
时,△OPQ面积的最大值为 ![]()
【解析】(1)设出椭圆的方程利用离心率且过点A求出几何量即可得出椭圆的标准方程。(2)设出直线的方程分别与椭圆的方程联立,求出P、Q的坐标即可得出结论。(3)根据题意设出PQ的直线方程代入椭圆方程利用弦长公式求出![]() 再求出原点到直线的距离即可得△OPQ的面积,然后利用基本不等式即可求出最大值。
再求出原点到直线的距离即可得△OPQ的面积,然后利用基本不等式即可求出最大值。

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目