题目内容
10. 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.(1)求证:DE∥平面A1B1C1;
(2)若平面ABC⊥平面BB1C1C,BB1=4,求三棱锥A-DCE的体积.
分析 (1)取棱A1C1的中点F,连接EF、B1F,利用三角形中位线定理,证明四边形DEFB1是平行四边形,从而DE∥B1F,利用线面平行的判定定理即可得出.
(2)过A作AH⊥BC于H,利用VA-DCE=VD-ACE=$\frac{1}{2}$${V}_{A-CD{C}_{1}}$,即可得出三棱锥A-DCE的体积.
解答 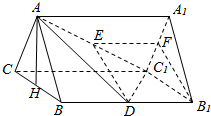 (1)证明:取棱A1C1的中点F,连接EF、B1F…(1分)
(1)证明:取棱A1C1的中点F,连接EF、B1F…(1分)
则由EF是△AA1C1的中位线得EF∥AA1,EF=$\frac{1}{2}$AA1
又DB1∥AA1,DB1=$\frac{1}{2}$AA1…(3分)
所以EF∥DB1,EF=DB1…(4分)
故四边形DEFB1是平行四边形,从而DE∥B1F…(5分)
所以DE∥平面A1B1C1…(6分)
(Ⅱ)解:因为E是AC1的中点,所以VA-DCE=VD-ACE=$\frac{1}{2}$${V}_{A-CD{C}_{1}}$…(7分)
过A作AH⊥BC于H…(8分)
因为平面平面ABC⊥平面BB1C1C,所以AH⊥平面BB1C1C,…(9分)
所以${V}_{A-CD{C}_{1}}$=$\frac{1}{3}×\frac{1}{2}×2×4×\sqrt{3}$=$\frac{4\sqrt{3}}{3}$…(11分)
所以VA-DCE=VD-ACE=$\frac{1}{2}$${V}_{A-CD{C}_{1}}$=$\frac{2\sqrt{3}}{3}$…(12分)
点评 本题考查三棱柱的性质、线面及面面平行与垂直的判定定理及其性质定理、三角形中位线定理、四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.双曲线$\frac{{x}^{2}}{25-k}$+$\frac{{y}^{2}}{9-k}$=1的焦距为( )
| A. | 16 | B. | 8 | ||
| C. | 4 | D. | 不确定,与k值有关 |
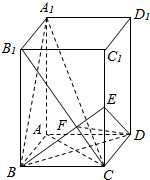 如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F.
如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F. 一个空间几何体的三视图及部分数据如图所示.
一个空间几何体的三视图及部分数据如图所示. 自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.
自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.