题目内容
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A.若m∥α,n∥α,则m∥n |
| B.若m∥α,m∥β,则α∥β |
| C.若m∥n,m⊥α,则n⊥α |
| D.若m∥α,α⊥β,则m⊥β |
C
试题分析:A同时平行于同一平面的两条直线不一定平行,可能相交,也可能是异面直线,∴A错误,B时平行于同条直线的两个平面,不一定平行,可能相交,∴B错误, C若m∥n,m⊥α,则根据直线平行的性质可知,n⊥α成立,C正确,D当m∥α,α⊥β,则m⊥β不一定成立,可能相交,可能平行,D错误,选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
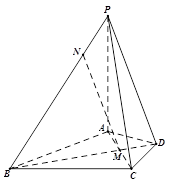
 ACD沿AC折起至
ACD沿AC折起至 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.

 平面BGH;
平面BGH;

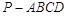 中,
中,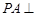 平面
平面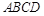 ,
,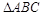 是正三角形,
是正三角形,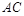 与
与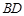 的交点
的交点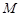 恰好是
恰好是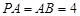 ,
,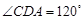 ,点
,点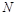 在线段
在线段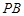 上,且
上,且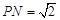 .
.
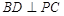 ;
;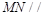 平面
平面 ;
;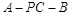 的余弦值.
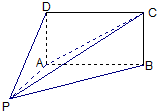
的余弦值.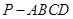 的底面
的底面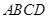 为矩形,且
为矩形,且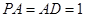 ,
,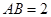 ,
,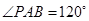 ,
,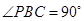 ,
,
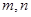 是两条不同的直线,
是两条不同的直线,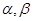 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
,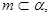
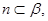 则
则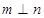
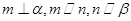 ,则
,则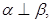
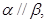
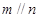
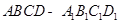 中,
中,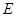 ,
,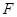 分别为棱
分别为棱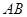 ,
,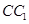 的中点,在平面
的中点,在平面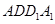 内且与平面
内且与平面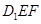 平行的直线( )
平行的直线( )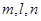 和平面
和平面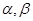 的四个命题:
的四个命题: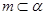 ,
,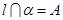 ,点
,点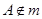 ,则
,则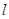 与
与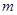 不共面;
不共面;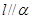 ,
,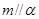 ,且
,且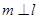 ,
,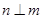 ,则
,则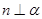 ;
;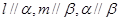 ,则
,则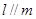 ;
;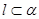 ,
,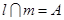 ,
,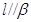 ,
,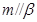 ,则
,则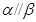 .
.